SOLUTION: An objective function and a system of linear inequalities representing constraints are given. Graph the system of inequalities representing the constraints. Find the value of the o

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: An objective function and a system of linear inequalities representing constraints are given. Graph the system of inequalities representing the constraints. Find the value of the o      Log On


   

Question 864643: An objective function and a system of linear inequalities representing constraints are given. Graph the system of inequalities representing the constraints. Find the value of the objective function at each corner of the graphed region. Use these values to determine the maximum value of the objective function and the values of x and y for which the maximum occurs.
Objective Function z = 11x - 25y
Constraints 0 ≤ x ≤ 5
0 ≤ y ≤ 8
4x + 5y ≤ 30
4x + 3y ≤ 20
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Graphing the system of inequalities representing the constraints:
The constraints 0%3C=x%3C=5 and 0%3C=y%3C=8
determine the rectangle whose sides are parts of the lines
x=0 , x=5 , y=0 , and y=8 in quadrant I.

The constraints 4x+%2B+5y%3C=30 and 4x+%2B+3y%3C=20
restrict the area further to the space below the lines
4x+%2B+5y=30 and 4x+%2B+3y=20 :

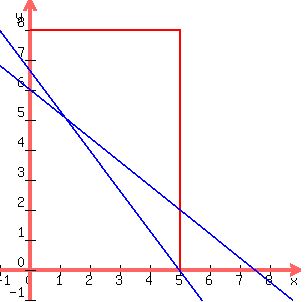
We know that it has to be below both lines, because point (0,0), the origin,
is a solution to both inequalities, 4x+%2B+5y%3C=30 and 4x+%2B+3y%3C=20 .
It is easy to draw those lines if you locate their x- and y-intercepts.
For 4x+%2B+5y=30 :
x=0-->4%2A0+%2B+5y=30-->0+%2B+5y=30-->5y=30-->y=30%2F5-->y=6 and
y=0-->4x+%2B+5%2A0=30-->4x%2B0=30-->4x=30-->x=30%2F4-->x=7.5
so those intercepts are (0,6) and (7.5,0).
For 4x+%2B+3y=20 :
x=0-->4%2A0+%2B+3y=20-->0+%2B+3y=20-->3y=20-->y=20%2F3-->y=6%262%2F3
y=0-->4x+%2B+3%2A0=20-->4x%2B0=20-->4x=20-->x=20%2F4-->x=5
so those intercepts are (0,20/3) and (5,0).

Finding the corners of the "graphed region:"
The graph tells us that points (0,0) , (0, 6) and (5,0) are three of the corners of the "graphed region."
The remaining corner is the intersection of 4x+%2B+5y=30 and 4x+%2B+3y=20 .
To find the coordinates of that point we solve system%284x+%2B+5y=30%2C4x+%2B+3y=20%29 .
We start by subtracting the second equation from the first to find y :
system%284x+%2B+5y=30%2C4x+%2B+3y=20%29-->system%284x+%2B+5y=30%2C2y=10%29-->system%284x+%2B+5y=30%2Cy=10%2F2%29-->system%284x+%2B+5y=30%2Chighlight%28y=5%29%29 .
Next, we substitute the value found for y in either equation, and solve to find x :
system%284x%2B5y=30%2Cy=5%29-->4x%2B5%2A5=30-->4x%2B25=30-->4x=30-25-->4x=5-->highlight%28x=5%2F4%29<-->highlight%28x=1.25%29 .
So the fourth and last corner is (1.25,5).

Finding the value of the objective function z+=+11x+-+25y at each corner:
At (0,0), z+=+11%2A0+-+25%2A0=highlight%280%29
At (0, 6), z+=+11%2A0+-+25%2A6=0-150=highlight%28-150%29
At (5,0), z+=+11%2A5+-+25%2A0=55-0=highlight%2855%29
At (1.25,5), z+=+11%2A1.25+-+25%2A5=13.75-125=highlight%28-111.25%29

Finding the maximum and its location:
Now that we have the value at the four corners of the region limited by the constraints,
we see that the function maximum is highlight%2855%29 at (5,0).

NOTE: The maximum (or minimum) of a linear function of x and y in a region that is a polygon must happen either at one corner, or at one edge.
If the greatest value found had been found at two corners, the entire edge connecting those two corners would have been the location of the maximum.