Question 785071: To deliver a message, an army officer will travel by car at 75mph from Camp A to Camp B, and then by plane to Camp C against a wind blowing 40 mph. The airplane can fly 280 mph in still air. If the messenger takes 3 2/3 hours in going from Camp A to Camp C and 3 1/6 hours for the return trip, what is the distance from Camp A to Camp C?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! To deliver a message, an army officer will travel by car at 75mph from Camp A to Camp B, and then by plane to Camp C against a wind blowing 40 mph.
The airplane can fly 280 mph in still air.
If the messenger takes 3 2/3 hours in going from Camp A to Camp C and 3 1/6 hours for the return trip,
what is the distance from Camp A to Camp C?
:
let x = dist from A to B
let y = dist from B to C
then
(x+y) = dist from A to C
:
We know the speed from A to B will be 75 mph both directions, however,
Speed from B to C will be 240 mph against the wind, and,
From C to B with the wind, it will be 320 mph
:
Change 2/3 to 4/6
:
Write a time equation for each trip
 + + 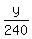 = 3 = 3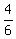
 + + 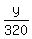 = 3 = 3
------------------------------------subtracting eliminates x, find y
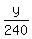 - - 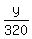 = = 
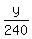 - - 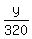 = = 
the common denominator of 960
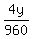 - - 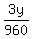 = = 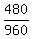
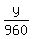 = = 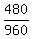
y = 480 miles from B to C
:
Find time from B to C
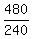 = 2 hrs = 2 hrs
:
Find time from A to B
3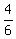 - 2 = 1 - 2 = 1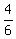 hrs which is hrs which is  hrs hrs
:
Find the dist from A to B
 * 75 = 125 miles * 75 = 125 miles
then
125 + 480 = 605 miles from A to C
:
:
:
See if that checks out; find the return trip time, use decimals this time
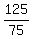 + + 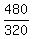 = =
1.67 + 1.5 = 3.17 which is about 3 hrs hrs
|
|
|