Question 761720: When will the parabola cross the x-axis with the equation y = 1/2 x-squared + 4x -2?
Answer by ramkikk66(644)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The key concept to remember is that for all points on the x axis, the y-coordinate is 0. i.e. y = 0 for all x on the x-axis.
At the point(s) where the parabola crosses the x axis, y will be 0.
In other words, 
Multiplying by 2 to get rid of the fraction in the left side

This is a standard quadratic equation of the for ax^2 + bx + c = 0 with a = 1, b = 8 and c = -4.
We can solve it using the quadratic solver as shown below. The graph also shows the 2 points where the parabola intersects the x axis.
The two points where it crosses the x axis are (0.4721,0) and (-8.4721,0)
:)
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=80 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 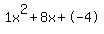 can be factored: can be factored:

Again, the answer is: 0.47213595499958, -8.47213595499958.
Here's your graph:
 |
|
|
|