y > 7
6x - y < -1
how do you know where do shade on a graph for those inequalities,
Immediately upon drawing each line, decide which side of
the line the shading will be on.
There are two methods, the "test point"-method and the
"solve for a letter"-method
(1)The test point method
Arbitrarily pick a point that is not on the line.
Substitute its x coordinate for x and it's y coordinate for y
in the inequality.
If this simplifies to a true numerical inequality, such as
-4 < -1 then the shading is on the side which the test point
is on.
If this simplifies to a false numerical inequality, such as
2 < -3 then the shading is on the side which the test point
is NOT on.
To make things easy as possible, you may very often, but not
always, choose the origin (0,0) You can do so if the line does
not pass through the origin. If it does choose another easy
point, like (0,±1) or (0,-1), (±1,0) or maybe (1,1)
--------------------------------------
The "Solve for a letter" method.
1. Solve for either x or y, remembering to
reverse the inequality when dividing by
a negative number to solve for the letter,
and not to reverse it when dividing by a
positive number.
2. If after solving for x, your inequality
begins " x > " or " x > ", then the shading
is on the RIGHT side of the line.
3. If after solving for x, your inequality
begins " x < " or " x < ", then the shading
is on the LEFT side of the line.
4. If after solving for y, your inequality
begins " y > " or " y > ", then the shading
is on the UPPER side of the line.
5. If after solving for y, your inequality
begins " y < " or " y < ", then the shading
is on the LOWER side of the line.
-----------------------------------------
I will demonstrate the "solve for a letter" method
For the first inequality y > 7
First we graph the boundary line, in green which is
y = 7. This is a horizontal line 7 units above the x-
axis and parallel to it.
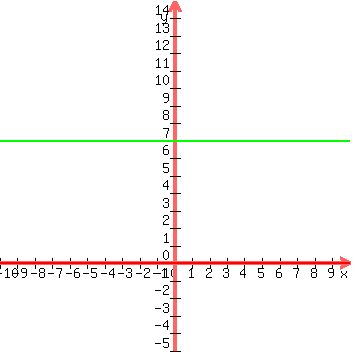That's supposed to be a dotted line, but I can only
draw it solid on here. Be sure to draw it dotted on
your paper, though.
The inequality y > 7 is already solved for y, and it
begins " y > ", so the shading is the UPPER side of the
green line.
For the second inequality 6x - y < -1
We graph its boundary line in blue, which is 6x - y = -1
This goes thru points (0,1) and (1,7)
The blue line should be dotted even tho it's solid
here. We must solve the inequality 6x - y < -1 for a letter.
If I choose to solve it for y
6x - y < -1
-y < -1 - 6x
y > 1 + 6x
it also begins " y > ", so the shading is on the UPPER
side of the blue line.
Notice that if I had instead chosen to solve it for x
instead
6x - y < -1
6x < -1 + y
x < -1/6 + y/6
It begins " x < ", so the shading is on the LEFT
side of the blue line.
The shading is on the same side either way, because
the UPPER side of the blue line and the LEFT side
of the blue line are the SAME SIDE of the blue line!
So you will shade the part that is ABOVE the green line
and on the LEFT and UPPER side of the blue line.
--------------------------------
and how do you find the exact intersection point?
Solve the system of equations consisting of the
two boundary lines:
y = 7
6x - y = -1
ny substitution. Do you know how to solve a system
of equations? If not, post again asking how.
Point of intersection: (1,7)
Edwin
