SOLUTION: If the lines passing through the points (1,a) and (4,-2) is parallel to the line passing through the points (2,8) and (-7,a+4), what is the value of a?

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: If the lines passing through the points (1,a) and (4,-2) is parallel to the line passing through the points (2,8) and (-7,a+4), what is the value of a?      Log On


   

Question 68019This question is from textbook Finite Mathmatics
: If the lines passing through the points (1,a) and (4,-2) is parallel to the line passing through the points (2,8) and (-7,a+4), what is the value of a? This question is from textbook Finite Mathmatics

Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
If the lines passing through the points (1,a) and (4,-2) is parallel to the line passing through the points (2,8) and (-7,a+4), what is the value of a?
:
Find the slopes using the slope equation: m = 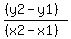%28%28y2-y1%29%29%2F%28%28x2-x1%29%29
:
The first given points: x1 = 1, y1 = a, x2 = 4, y2 = -2, call the slope m1:
m1 = 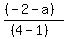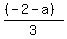%28%28-2+-+a%29%29%2F%28%284+-+1%29%29 = %28%28-2-a%29%29%2F3
:
The 2nd given points: x1 = 2, y1 = 8, x2 = -7, y2 = (a+4); call the slope m2
m2 = 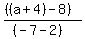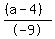%28%28%28a%2B4%29+-+8%29%29%2F%28%28-7+-+2%29%29 = %28%28a+-4%29%29%2F-9
When lines are parallel, slopes are equal, m1 = m2 so we have:
:
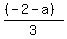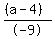
%28%28-2-a%29%29%2F3 = %28%28a+-+4%29%29%2F-9
:
Cross multiply and solve for a
-9(-2-a) = 3(a - 4)
18 + 9a = 3a - 12
9a - 3a = -12 - 18
6a = -30
a = -30/6
a = -5
:
:
You can check the solution by finding the 2 slopes to see if they are equal.