Question 6664: Dear Sir/Madam,
I am confronted with the following problem:
"Let parallelogram ABCD have vertices on the xy-coordinate plane A(0,0), B(b,0), and C(a,c). Find an equation for the distances between the points B and D. Assume a, b, and c are all positive and assume a > b."
I visualize this parallelogram (well, at least partially) and have drawn myself a sketch of it, but how would you go about solving this question because I can't seem to figure it out?!
Thanks in advance.
Regards,
-Mike
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! It's tough to show you how this works if I can't show you a drawing. For sure, though, you know that point B lies further to the positive direction along the x-axis from A, so segment AB forms the very base of your parallelogram. They said that point C is at (a,c). If a > b, then point C is further to the right (positive direction) than point B, and it's c units above the x-axis. If you connect a line from AB and then from BC, you should get an obtuse angle opening "northwest".
The trick here is getting the coordinates of point D, the missing point that would complete the parallelogram. Since we now know that CD must be parallel to AB, the y-coordinate of point D must be c. So far, the coordinate point of point D is (?,c). We don't know yet what D's x-coordinate is.
Examine the diagonal segment BC (the right edge of the parallelogram). Its slope is  which actually is which actually is 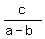 . We'll have to examine the (a - b) because that's the change in x from point B to point C. The change in x from point A to point D MUST also be the same change in x as the one from point B to point C. That way, BC and AD are parallel. So, from point A, which is coodinate point (0,0), we need to shift-copy the x-coodinate by (a - b) (to the right) and bring that "copy" up vertically by c so that it's horizontally aligned with point C. This makes point D have the coordinate point (a-b,c). . We'll have to examine the (a - b) because that's the change in x from point B to point C. The change in x from point A to point D MUST also be the same change in x as the one from point B to point C. That way, BC and AD are parallel. So, from point A, which is coodinate point (0,0), we need to shift-copy the x-coodinate by (a - b) (to the right) and bring that "copy" up vertically by c so that it's horizontally aligned with point C. This makes point D have the coordinate point (a-b,c).
Now, we have to plug in the x and y values from point C and D to the distance formula:
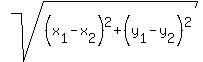 <----- formula <----- formula
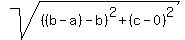 <---- plugged values in. <---- plugged values in.
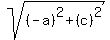 <---- further simplification. <---- further simplification.
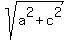 <---- This ultimately should be the expression for the distance between points C and D. <---- This ultimately should be the expression for the distance between points C and D.
|
|
|