Question 6647: Dear Sir/Madam,
I am confronted with the following problem:
"Find the equation of the line that is tangent to the circle x^2 + y^2 = 25 at the point P(-3,4)."
I did the following:
1) 
2) 
3) f'(x) =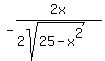 
4) f'(-3) = 
5) 
6) -3(x + 3) = 4(y - 4)
7) -3x - 9 = 4y - 16
8) 4y = -3x + 7
9)  which should be the equation of the tangent.
Instead however,  is the equation of the tangent. Why?
Thanks in advance.
Regards,
-Mike
Found 2 solutions by rapaljer, Mike:
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! Your problem is in step 2, where you solved for y by taking the square root of both sides of the equation. You must include a "+ or -" symbol in this step, where the plus or the minus is determined by the point that is selected. What you have is the equation of a circle, and the point of tangency is at (-3,4) placing the point in the second quadrant, since x is negative and y is positive. Notice that in the second quadrant, the slope of a tangent line to a point on the curve will have a positive slope (by inspection!), so you have to use the plus sign for the slope of the tangent line. In quadrant IV, where x is positive and y is negative, you also have a positive slope. In quadrants I and III, the tangent line to a circle will have a negative slope (again by inspection!).
I think the rest of what you have done is correct.
R^2 at SCC
Answer by Mike(39)  (Show Source):
|
|
|
