Question 62098: 2 trains left the same city at the same time, traveling in opposite directions. the eastbound train traveles for 10 hours, and the westbound train traveles for 5 hours. They are now 1300 km. apart. the westbound train's rate is 20 km/h faster than the eastbound train. Find the rate of the speed of each train.
Found 2 solutions by ankor@dixie-net.com, joyofmath:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2 trains left the same city at the same time, traveling in opposite directions. the eastbound train travels for 10 hours, and the westbound train travels for 5 hours. They are now 1300 km. apart. the westbound train's rate is 20 km/h faster than the eastbound train. Find the rate of the speed of each train.
:
Let s = speed of the slower train:
Then (s+20) = speed of the faster train
:
Dist = time * speed
:
Eastbound dist + westbound dist = 1300
10s + 5(s+20) = 1300
10s + 5s + 100 = 1300
15s = 1300 - 100
15s = 1200
s = 1200/15
s = 80 mph for slow one and 100 mph for the fast one
:
Check 80*10 + 100*5 = 1300
:
How about this? Did it make sense to you?
Answer by joyofmath(189)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2 trains left the same city at the same time, traveling in opposite directions. the eastbound train traveles for 10 hours, and the westbound train traveles for 5 hours. They are now 1300 km. apart. the westbound train's rate is 20 km/h faster than the eastbound train. Find the rate of the speed of each train.
Let 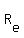 = the rate (or speed) of the eastbound train. = the rate (or speed) of the eastbound train.
Let 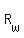 = the rate (or speed) of the westbound train. = the rate (or speed) of the westbound train.
Let 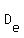 = the distance covered by the eastbound train. = the distance covered by the eastbound train.
Let 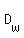 = the distance covered by the westbound train. = the distance covered by the westbound train.
Distance = Rate x Time.
We know that the eastbound train traveled for 10 hours.
So,  . .
We know that the westbound train traveled for 5 hours.
So,  . .
We know that the total distance covered = 1300 so  . .
Or,  . .
We know that the westbound rate is 20 km/hour faster than the westbound rate.
So,  . .
So,  . .
Or,  . .
Or,  . .
Or,  . .
So,  . .
So, the eastbound train is going 80 km/hour and the westbound train is going 100 km/hour.
Verify:
In 10 hours, the eastbound train covers 10*80 km = 800 km.
In 5 hours, the westbound train covers 5*100 km = 500 km.
The total distance = 800 + 500 = 1300 km which is what the problem stated.
|
|
|