SOLUTION: I need help solving this problem: {{{ 7y^3-27y^2-4y=0 }}} I've already factored out the y, but after that I'm not sure what I'm supposed to do, I used the quadratic formula but I

You are supposed to find all values of y which, when substituted
for y, the equation is true, i.e., it comes out 0 = 0.

 7y³ - 27y² - 4y = 0

Factor out the y, and you have this:

y(7y² - 27y - 4) = 0

Now factor the expression in the parentheses:

y(y - 4)(7y + 1) = 0

Since the right sides is 0, any one of those three factors 
on the left can equal 0 and the equation will be true.

The first factor on the left is y.

So y = 0 is a solution

The second factor on the left is y - 4

We set it = 0 and get y = 4

So y = 4 is also a solution.

The third factor on the left is 7y + 1

We set it = 0 and get y =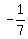 

So y =  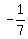is also a solution.


Therefore there are three values of y which,
when substituted for y in the equation

7y³ - 27y² - 4y = 0

the equation is true, i.e., it comes out 0 = 0.

So the three solutions are 

0, 4, and 

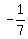Edwin