2x - 2y - 4z = -2
3x - 3y - 6z = -3
-2x + 3y + z = 7
It is true that if you try to eliminate any variable in 1&2
everything cancels out. This means there are infinitely
many solutions, but we can still find the general solution.
So try to eliminate a letter using 2&3. Notice that the y's
will cancel if you add 2&3 as they are:
3x - 3y - 6z = -3
-2x + 3y + z = 7
------------------
x - 5z = 4
So solve for x:
x = 4 + 5z
Substitute 4 + 5z for x in either 1 or 2. I'll pick 1
2x - 2y - 4z = -2
2(4+5z) - 2y - 4z = -2
8 + 10z - 2y - 4z = -2
8 + 6z - 2y = -2
Solve for y:
-2y = -10 - 6z
y =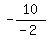 
- 
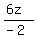y = 5 + 3z
So the general solution is
x = 4 + 5z, y = 5 + 3z, z = z
often written as a 3D point:
(x, y, z) = (4+5z, 5+3z, z)
There are infinitely many solutions.
To get some of them, substitute arbitrary values for z:
Substitute, say, 1 for z:
(x, y, z) = (4+5z, 5+3z, z) = (4+5·1, 5+3·1, z) = (9, 8, 1)
Substitute, say, -2 for z:
(x, y, z) = (4+5z, 5+3z, z) = (4+5·-2, 5+3·-2, z) = (4-10, 5-6, -2) = (-6, -1, -2)
You can get as many different solutions as you like just by
substituting arbitrary values for z.
Edwin
