2x + 4y - 3z = -8
3y + 2z + 6x = 3
4z - 8x - 7y = 5
Rearrange the terms on the left so that the terms are
all in alphabetical order with the letters:
(A) 2x + 4y - 3z = -8
(B) 6x + 3y + 2z = 3
(C) -8x - 7y + 4z = 5
Pick a letter to eliminate and two of the equations to
eliminate it from:
I will pick the letter x to eliminate and I will pick
(A) and (B) to eliminate it from:
I will multiply (A) by -3 and add (B) to it
-6x - 12y + 9z = 24
(B) 6x + 3y + 2z = 3
------------------------------
(D) -9y + 11z = 27
Eliminate the SAME letter from a different pair of equations,
[that is, you will choose the equation you did not choose before
along with one of the equations that you did choose before.]
I will pick (A) and (C) to eliminate the SAME letter x from:
I will multiply (A) by 4 and add (C) to it
8x + 16y - 12z = -32
(C) -8x - 7y + 4z = 5
-------------------------------
(E) 9y - 8z = -27
Now we have reduced the 3 equations and 3 unknowns down
to just 2 equations (D) and (E) and 2 unknowns:
(D) -9y + 11z = 27
(E) 9y - 8z = -27
The y's will eliminate by just adding them as they are:
(D) -9y + 11z = 27
(E) 9y - 8z = -27
------------------------------
3z = 0
z =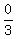 
z = 0
Substitute z = 0 in (E)
9y - 8(0) = -27
9y - 0 = -27
9y = -27
y = -3
Substitute y = -3 and z = 0 into one of the originals.
I'll pick (A)
(A) 2x + 4y - 3z = -8
2x + 4(-3) - 3(0) = -8
2x - 12 - 0 = -8
2x - 12 = -8
2x = 4
x = 2
Solution: (x,y,z) = (2,-3,0)
Edwin
