Question 417759: A manufacturer produces three types of radios: deluxe, standard and economy. Each radio uses three different types of transistors: P, Q and R. The deluxe radio uses 2 P's, 7 Q's and 1 R. The standard contains 2 P's, 3 Q's and 1 R, and the economy model requires 1 P, 2 Q's and 2 R's.
How many radios of each type can be constructed if the total number of transistors (P's, Q's and R's) available are 2200, 3400 and 1400 respectively and all transistors must be used?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A manufacturer produces three types of radios: deluxe, standard and economy.
Each radio uses three different types of transistors: P, Q and R.
The deluxe radio uses 2 P's, 7 Q's and 1 R.
The standard contains 2 P's, 3 Q's and 1 R, and
the economy model requires 1 P, 2 Q's and 2 R's.
How many radios of each type can be constructed if the total number of transistors (P's, Q's and R's) available are 2200, 3400 and 1400 respectively and all transistors must be used?
:
Let d = no. of deluxe radios
Let s = no. of standard radios
let e = no. of cheap radios
:
Write a equation for each type of transistor
2d + 2s + 1e = 2200; the P trans
7d + 3s + 2e = 3400; the Q trans
1d + 1s + 2e = 1400; the R trans
:
multiply the 3rd equation by 2, subtract the 1st equation
2d + 2s + 4e = 2800
2d + 2s + 1e = 2200
---------------------subtraction eliminates d and s, find e
0d + 0s + 3e = 600
e = 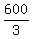
e = 200 cheap radios
:
Using the first two equations, replace e with 200
2d + 2s + 200 = 2200
2d + 2s = 2200 - 200
2d + 2s = 2000
and
7d + 3s + 2(200) = 3400
7d + 3s = 3400 = 400
7d + 3s = 3000
:
Multiply the above equation by 2, the 1st two unknown equation by 3
14d + 6s = 6000
6d + 6s = 6000
-----------------Subtraction eliminates s, find d
8d = 0; this means that there will be no deluxe radios
:
Find s using the 1st equation: 2d + 2s + 1e = 2200;
2(0) + 2s + 200 = 2200
2s = 2200 - 200
2s = 2000
s = 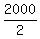
s = 1000 standard radios
:
I'm going to say the in order to use all the available transistors, you have
0 deluxe radios
1000 standard radios
200 cheap radios
:
This checks out in all three equations.
|
|
|