Question 316769: Could someone help me with this problem? I am confused?
Bayside Insurance offers two health plans. Under Plan A, Sam would have to pay the first $80 of his medical bills, plus 35% of the rest. Under Plan B, Sam would pay the first $230, but only 20% of the rest. For what amount of medical bills will Plan B save Sam money? Assume he was over $230 in bills. Sam would save with Plan B if he had more than $_____ in bills.
Found 2 solutions by ankor@dixie-net.com, Fombitz:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Bayside Insurance offers two health plans. Under Plan A, Sam would have to pay the first $80 of his medical bills, plus 35% of the rest.
Under Plan B, Sam would pay the first $230, but only 20% of the rest.
:
Let b = amt of the medical bill
Let p = amt he has to pay after insurance pays
:
Write an equation for plan A
p = .35(b-80) + 80
:
Write an equation for plan B
p = .20(b-230) + 230
:
For what amount of medical bills will Plan B save Sam money?
Assume he was over $230 in bills.
Sam would save with Plan B if he had more than $_____ in bills.
:
Plan A amt > Plan B amt
.35(b-80) + 80 > .20(b-230) + 230
.35b - 28 + 80 > .20b - 46 + 230
.35b + 52 > .20b + 184
.35b - .20b > 184 - 52
.15b > 132
b > 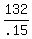
b > $880, when his bill exceeds $880, he would save money with plan B
:
:
It will help you understand, if you substitute 880 for b in both equations
and find out the actual amt he will pay
Answer by Fombitz(32388)   (Show Source): (Show Source):
|
|
|