Question 289444: I hate word problems, but here it goes.
The owner of a tea shop wants to mix three kinds of tea to make 100 oz of a mixture that will sell for $0.83 per oz. He uses Orange Pekoe, which sells for $0.80 per oz, Irish Breakfast, for $0.85 per oz, and Earl Grey, for $0.95 per oz. If he wants to use twice as much Orange Pekoe as Irish Breakfast, how much of each kind of tea should he use?
So far these are the equations I have come up with:
x + y + z = 100
0.80x + 0.85y + 0.95z = 0.83
x = 2y
I plugged in x = 2y into the first equation, like this:
2y + y + z = 100
But I still need to get rid of the z. So I add 2y + 1y and solve for z, which gives me z = -3y + 100 and then I plug it into the first equation again, so that I get this: 2y + y + -3y + 100 = 100
But it cancels out. What am I doing wrong? How do I solve this problem?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The owner of a tea shop wants to mix three kinds of tea to make 100 oz of a mixture that will sell for $0.83 per oz. He uses Orange Pekoe, which sells for $0.80 per oz, Irish Breakfast, for $0.85 per oz, and Earl Grey, for $0.95 per oz. If he wants to use twice as much Orange Pekoe as Irish Breakfast, how much of each kind of tea should he use?
So far these are the equations I have come up with:
x + y + z = 100
:
This equation should be
0.80x + 0.85y + 0.95z = 0.83(100)
x = 2y
I plugged in x = 2y into the first equation, like this:
2y + y + z = 100
3y + z = 100
then
z = (100-3y)
:
Substitute for x and z in the cost equation, find y
0.80x + 0.85y + 0.95z = 0.83(100)
.8(2y) + .85y + .05(100-3y) = 83
1.6y + .85y + 5 - .15y = 83
1.6y + .85y - .05y = 83 - 5
2.6y = 78
y = 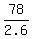
y = 30 oz of Irish tea
:
I'm sure you can find x and z now,
:
Note, remember you cannot substitute in the same equation that you derived
substitution expression from. If you do, that's what happens.
Always substitute in the "other" equation.
:
Check your 3 solutions in the two original equations.
|
|
|