Question 236336: I was asked to simplify this 4z to the eighth power z to the -6 power y to the -9 power times 5y to the -1 power w to the -7 power times 2w to the 7th power
i have not had math for over 30 years stuck bad. Do you also know of any websites that gives free help and explanation of problems and rules.
Any help greatly appreciated
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here are some good ones.
http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/index.htm
http://www.purplemath.com/lessons.htm
http://tutorial.math.lamar.edu/Classes/Alg/Alg.aspx
http://www.jamesbrennan.org/algebra/
There's tons of stuff on the internet. Just do a search on "algebra" or "algebra lessons" or "algebra tutorials".
Some are pay sites and some are free. The ones above are free.
Algebra.com also has lessons.
You can scan down their home page using the search word "lessons" and down at the bottom towards the right you should find a link.
Here's a link that will guide you if it works.
http://www.algebra.com/tutors/all-lessons.mpl
There are also video lessons.
If you're going to use algebra.com, then some of the terminology that would be helpful is:
x*y means x multiplied by y
x/y means x divided by y
x^y means x raised to the power of y
root(n,x) means the nth root of x
sqrt(x) means the square root of x
a*(b+d) means do the addition first, then multiply
A couple of rules for exponents might help.
x^y*x^z = x^(y+z) example 3^2*3^3 = 3^(2+3) = 3^5
x^y/x^z = x^(y-z) example 3^5/3^2 = 3^(5-2) = 3^3
(x^y)^z = x^(y*z) example (3^2)^3 = 3^(2*3) = 3^6
x^(n/z) = root(z,x)^n example 3^(6/3) = root(3,3)^6 = root(3,3^6) = 3^2 = 9
x^(1/y) = root(y,x) example 27^(1/3) = root(3,27) = 3
x^(-n) = 1/x^n example 3^(-3) = 1/3^3 = 1/27
x*y*z = x*(y*z) = (x*y)*z = z*(y*x) = y*(z*x) example 1*2*3 = 1*(6) = (2)*3 = 3*(2) = 2*(3) with the terms in parentheses being multiplied first.
Your problem is:
Simplify 4z to the eighth power z to the -6 power y to the -9 power times 5y to the -1 power w to the -7 power times 2w to the 7th power
I had a little trouble understanding it.
This is what I think it is and how to simplify it.
4*z^8*z^(-6)*y^(-9)*5*y^(-1)*w^(-7)*2*w^7
If you put it through the algebra.com formula generator, it will look like this:
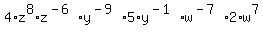
4z^8*z^(-6) = 4*z(8-6) = 4*z^2
y^(-9) * 5 * y^(-1) = 5*y^(-9)*y^(-1) = 5*y^(-9-1) = 5*y^(-10)
w^(-7)*2*w^7 = 2*w^(-7)*w^7 = 2*w^(-7+7) = 2*w^0 = 2*1 = 2
Your whole equation should then become:
4z^2*5y^(-10)*2
This can be re-ordered to be:
4*5*2*z^2*y^(-10)
This becomes:
40*z^2*y^(-10)
This becomes:
40z^2/y^10
To prove this is correct, then pick some values for z, y, w, and solve the original equation and solve the final equation. If they match, then the simplification was good.
Let z = 2, y = 3, w = 4
Your final equation of 40z^2/y^10 becomes:
40*(2)^2/3^10 = 160/59049 (from final equation)
Your original equation of
4*z^8*z^(-6)*y^(-9)*5*y^(-1)*w^(-7)*2*w^7 becomes:
4*(2)^8*(2)^(-6)*(3)^(-9)*5*(3)^(-1)*(4)^(-7)*2*(4)^7
This becomes:
1024 * (1/64) * (1/19683) * (5/3) * (1/16384) * 32768
This becomes:
(1024 * 5 * 32768) / (64 * 19683 * 3 * 16384)
This becomes:
(1024 * 5 * 2) / (64 * 19683 * 3)
This becomes:
(16 * 5 * 2) / (19683 * 3)
This becomes:
160 / 59049 (from original equation)
The answers match so the simplification looks good.
|
|
|