
Multiply row 1 thru by -2 and add to row 2
 Multiply row 1 by -1 and add to row 3
Multiply row 1 by -1 and add to row 3
 Multiply row 2 by -1 and add to row 3
Multiply row 2 by -1 and add to row 3
 Now we write the system of equations that this
matrix represents:
Now we write the system of equations that this
matrix represents:
 The bottom equation is all 0's so any values of
x, y, and z would be solutions to it, so we eliminate
it
Choose an arbitrary value for z, we will use
The bottom equation is all 0's so any values of
x, y, and z would be solutions to it, so we eliminate
it
Choose an arbitrary value for z, we will use  Or, after erasing the 0s and 1 coefficients:
Or, after erasing the 0s and 1 coefficients:
 Substitute
Substitute  for
for  in the 2nd equation:
in the 2nd equation:
 Solve for y
Solve for y

 Substitute
Substitute  for
for  and
and 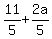 for
for  in the first equation:
in the first equation:


 Clear of fractions:
Clear of fractions:



 So the solution is:
(x, y, z) = (
So the solution is:
(x, y, z) = (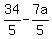 ,
,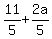 ,
, )
Edwin
)
Edwin