Question 206014: 3/4=1-3x-2/x+1
really means 3/4 = 1 - (3x-2)/(x+1) ?
Answer by mickclns(59)   (Show Source): (Show Source):
You can put this solution on YOUR website! Notice the edited version of your question. PLEASE, ALL QUESTIONERS TAKE NOTE: when a fraction is in vertical form, the horizontal division line acts as a grouping operator -- that means: WHEN YOU CONVERT IT INTO HORIZONTAL FORM YOU ***MUST*** USE PARENTHESES TO HAVE IT CONTINUE TO MEAN THE SAME THING.
So, first, the solution to what your question means as written:
 subtract 2 from both sides subtract 2 from both sides
 multiply both sides by 4x to get rid of the fractions multiply both sides by 4x to get rid of the fractions
 add add 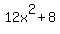 to both sides to both sides

To see whether this factors, look at the discriminant (what's under the square root in the quadratic formula)
 Since this number is negative, this quadratic expression is not factorable (the discriminant must be a perfect square for the quadratic to be factorable). Since this number is negative, this quadratic expression is not factorable (the discriminant must be a perfect square for the quadratic to be factorable).
Using the quadratic formula, then,
 --> --> 
 , a = 12, b=-5, c = 8 (notice you can only use this when one side is 0) , a = 12, b=-5, c = 8 (notice you can only use this when one side is 0)

 , which, since 359 is prime is as simple as it gets. , which, since 359 is prime is as simple as it gets.
OK, now what the problem was probably intended to be (correct me if I'm wrong, I'm not at all certain):
 To get rid of fractions, multiply both sides by 4(x+1) To get rid of fractions, multiply both sides by 4(x+1)
 quick simplification of each side ( on right side 4(x-1) is multiplied by both terms) quick simplification of each side ( on right side 4(x-1) is multiplied by both terms)
 next step of simplification: multiplying out next step of simplification: multiplying out
 to get x's and constants on opposite sides, add 8x - 3 to both sides to get x's and constants on opposite sides, add 8x - 3 to both sides
 so so 
|
|
|