SOLUTION: The points (1, 3), (2, 5), (8, 17), (50, 101), and (1000, 2001) all lie on line M. The points (1, -1), (2, -3), (8, -15), (50, -99), and (1000, -1999) all lie on line N. a. Form

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: The points (1, 3), (2, 5), (8, 17), (50, 101), and (1000, 2001) all lie on line M. The points (1, -1), (2, -3), (8, -15), (50, -99), and (1000, -1999) all lie on line N. a. Form       Log On


   

Question 203229: The points (1, 3), (2, 5), (8, 17), (50, 101), and (1000, 2001) all lie on line M.
The points (1, -1), (2, -3), (8, -15), (50, -99), and (1000, -1999) all lie on line N.
a. Form the equations of both the lines. Show your work.
b. What are the co-ordinates of the point of intersection of lines M and N?
c. Write the co-ordinates of the intersections of lines M and N with the x-axis.
d. Write the co-ordinates of the intersection of lines M and N with the y-axis. Could you help me with these? This is very difficult for me. You are very much appreciated.
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Since we are talking about linear equations, we need only two points to define the line and we can write the equation of the line if we know its slope and its y-intercept.
We can write the equations in the slope-intercept form: y = mx+b where m = slope and b = y-intercept.
For line M, pick any two of the given five points to find the slope (m) of the line:
m+=+%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29 Let's pick the first two points from the list (1, 3) and (2, 5) and substitute their x- and y-cordinates into the slope formula:
m+=+%285-3%29%2F%282-1%29
m+=+2%2F1
m+=+2 so, we have, so far...
y+=+2x%2Bb To find b, the y-intercept, you can use the x- and y-coordinates of either one of the two points (or any of the other given points for that matter, as long as they lie on the line). Let's use the first point in the list (1, 3):
3+=+2%281%29%2Bb Subtract 2 from both sides of the equation.
1+=+b so the final equation for line M is:
highlight%28y+=+2x%2B1%29
Similarly, for line N:
m+=+%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29 Pick points (1, -1) and (2, -3), substitute their x- and y-coordinates:
m+=+%28-3-%28-1%29%29%2F%282-1%29
m+=+%28-3%2B1%29%2F1%29
m+=+-2 so...
y+=+-2x%2Bb use the second point (2, -3) to find b, substitute:
-3+=+-2%282%29%2Bb
-3+=+-4%2Bb Add 4 to both sides.
1+=+b so the final equation for line N is:
highlight_green%28y+=+-2x%2B1%29
-------------------------------------
The point of intersection of the two lines is found by solving the system of linear equations just developed. This is esily done by setting the two equations equal and solving for x.
2x%2B1+=+-2x%2B1 Add 2x to both sides.
4x%2B1+=+1 Subtract 1 from both sides.
4x+=+0so...
x+=+0 now substitute this into either one of the two equations and solve for y:
y+=+2%280%29%2B1
y+=+1
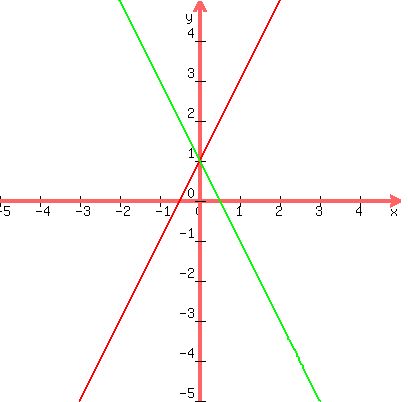
The point of intersection of the two lines is (0, 1)
--------------------------------------------
The line intersect the x-axis at y = 0, so, set y = 0 in each equation and solve for x.
For line M:
y+=+2x%2B1 Substitute y = o.
0+=+2x%2B1 Subtract 1 from both sides.
-1+=+2x Divide both sides by 2.
-1%2F2+=+x or highlight%28x+=+-1%2F2%29
For line N:
y+=+-2x%2B1 Substitute y = 0.
0+=+-2x%2B1 Subtract 1 from both sides.
-1+=+-2x Divide both sides by -2.
1%2F2+=+x or highlight_green%28x+=+1%2F2%29
---------------------------------------
Remember that the intersection of the lines with the y-axis is called the y-intercept or b in the equation of the lines.
Foe line M: b = 1.
For line N: b = 1.
----------------------------------
graph%28400%2C400%2C-5%2C5%2C-5%2C5%2C2x%2B1%2C-2x%2B1%29