Question 200854: The Jurassic Zoo charges $28.00 for each adult admission and $12.00 for each child. The total bill for 254 people from a school trip was $3864.00. How many adults and how many children went to the zoo?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let
a = # of adults that attended
c = # of children that attended
Since a total of 254 people attended, this means that  . Also, because "The Jurassic Zoo charges $28.00 for each adult admission and $12.00 for each child" and "The total bill for 254 people from a school trip was $3864.00", we know that . Also, because "The Jurassic Zoo charges $28.00 for each adult admission and $12.00 for each child" and "The total bill for 254 people from a school trip was $3864.00", we know that 
So we have the system of equations:

In order to solve for one variable, we must eliminate the other variable. So if we wanted to solve for "a", we would have to eliminate "c" (or vice versa).
So lets eliminate "c". In order to do that, we need to have both "c" coefficients that are equal but have opposite signs (for instance 2 and -2 are equal but have opposite signs). This way they will add to zero and cancel out.
So to make the "c" coefficients equal but opposite, we need to multiply both "c" coefficients by some number to get them to an equal number. So if we wanted to get 1 and 12 to some equal number, we could try to get them to the LCM 12. However, we want one number equal to 12 and the other equal to -12.
Because one "c" coefficient is already equal to 12, we need to multiply both sides of the first equation by -12 (to get the "c" coefficient equal to -12).
 Start with the first equation. Start with the first equation.
 Multiply the both sides of the first equation by -12. Multiply the both sides of the first equation by -12.
 Distribute and multiply. Distribute and multiply.
So we have the new system of equations:

Take note that the "c" coefficients are equal but opposite.
Now add the equations together. You can do this by simply adding the two left sides and the two right sides separately like this:

 Group like terms. Group like terms.
 Combine like terms. Combine like terms.
 Simplify. Simplify.
 Divide both sides by Divide both sides by  to isolate to isolate  . .
 Reduce. Reduce.
------------------------------------------------------------------
 Now go back to the first equation. Now go back to the first equation.
 Plug in Plug in  . .
 Multiply. Multiply.
 Add Add 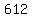 to both sides. to both sides.
 Combine like terms on the right side. Combine like terms on the right side.
 Divide both sides by Divide both sides by  to isolate to isolate  . .
 Reduce. Reduce.
============================================================================
Answer:
So the solutions are  and and  . .
This means that 51 adults attended and 203 children attended.
|
|
|