Question 177644: Russ and Janet are running in the Apple Hill Fun Run. Russ runs at 7 mph, Janet runs at 5 mph. If they start at the same time, how long will it be before they are half a mile apart? show me step by step..
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since Russ is running at 7 mph, and Janet at 5 mph, in 1 hour, they would be 2 miles apart.
Using this info., we can then utilize proportions to figure out the time that it tales them to get to distances that are 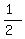 , or .5 miles apart. , or .5 miles apart.
Therefore, we have: 
2a = .5
a = .25
Therefore, it takes .25 hour, or 15 minutes for Russ and Janet to be 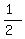 , or .5 of a mile apart. , or .5 of a mile apart.
Checking:
In 15 mins, or .25 hr, Russ will be 1.75 (.25 x 7) miles away from the starting point.
In 15 mins, or .25 hr, Janet will be 1.25 (.25 x 5) miles away from the starting point.
Therefore, they will be .5 (1.75 – 1.25) of a mile apart, 15 minutes, or .25 hr after starting their run.
|
|
|