Question 173842This question is from textbook finite math with application
: A shop sells skirts for $45 and blouses for $35. Its entire stock is worth $51,750, but sales are slow and only half the skirts and two-thirds of the blouses are sold, for a total of $30,600. How many skirts and blouses are left in the store?
This question is from textbook finite math with application
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! shop sells skirts for $45 and blouses for $35. Its entire stock is worth $51,750, but sales are slow and only half the skirts and two-thirds of the blouses are sold, for a total of $30,600. How many skirts and blouses are left in the store?
---------------
Equations:
Value equation: 45s + 35b = 51750
Value equation: (1/2)45s + (2/3)35b = 30600
------------------------------
9s + 7b = 10350
22.5s + 23.333b = 30600
----------------------------
Solve by what ever method you know to get:
s = 520 (original number of skirts)
b = 810 (original number of blouses)
--------------
skirts now in the store: (1/2)520 = 260
blouses now in the store: (1/3)810 = 270
=============================================
Cheers,
Stan H.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Generally, I select my variables for word problems so that what I am solving for is the required answer. But in this case, it seems more straightforward to solve for the number of skirts and blouses in inventory at the start.
So:  is the beginning number of skirts, and is the beginning number of skirts, and  is the beginning number of blouses. is the beginning number of blouses.
We know that the value of all the skirts at the beginning must be  and the value of all the blouses must be and the value of all the blouses must be 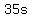 . Furthermore we know that the value of the entire inventory is $51,750. . Furthermore we know that the value of the entire inventory is $51,750.
So we can write:  (Eq. 1) (Eq. 1)
The value of the one-half of the skirts that sold must be 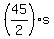 and the value of the two-thirds of the blouses that sold must be and the value of the two-thirds of the blouses that sold must be 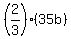 and the sum of these two expressions must be the total revenue, or $30,600. and the sum of these two expressions must be the total revenue, or $30,600.
Now we can write:  (Eq. 2) (Eq. 2)
Multiply Equation 2 by -6:
 (Eq. 3) (Eq. 3)
Multiply Equation 1 by 4:
 (Eq. 4) (Eq. 4)
Add Equation 3 and Equation 4, term by term:



Take this value for  and substitute into Equation 1: and substitute into Equation 1:



So, the store started with 520 skirts, but sold half of them, leaving 260 in stock. Also, the store started with 810 blouses, but sold two-thirds of them, leaving one-third in stock  . .
|
|
|