Question 170032: Hi, Can you please help?
.
When given the system of equations of
.
If you are solving it using elimination
.
This is how I would solve it
.
I would multiply the whole second equation by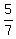 
.
 =  = 
.
I would then add this equation with the first equation
.
.
I would then come up with  , then I solve it, and find that "x" = 2, then I would plug in the answer, and find that "y" = (-1)
.
Is this how elimination works?
.
Or do you have to do it this way...
.
.
Multiply the first equation by "7" and the second by "5"
.
I did the math and came up with
.
.
Then add the equations
.
I get  , and then find "x" is "2", and "y" = (-1)
.
I will be doing quizzes soon, and I perfer the first way, but does elimination mean you do it the second way
.
What I am asking is, is it o.k. to do elimination the first way, or is the second way, the right way to do it?
.
Thanks ahead of time, Levi
Answer by checkley77(12844)   (Show Source):
You can put this solution on YOUR website! IF BOTH MATHODS GETS YOU THE CORRECT ANSWERS THEN YOU SHOULD CHOOSE THE SHORTEST METHOD. LESS CHANCE OF MAKING A MISTAKE IN THE MATH & YOU'RE USING WHOLE NUMBERS RATHER THAN FRACTIONS (WHICH CAN GET MESSY OR CONFUSING).
|
|
|
