Problem:
Suppose $8,000 is invested at interest rate k, compounded continuously, and grows to $11,466.64 in 6 years.
a) Find the interest rate
where 
, 
, 
Divide both sides by 
Take natural logs of both sides:
Use fact that 
Divide both sides by 6:
Use calculator:
We'll round that to 
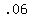or 
---------------------
b) Find the exponential growth function
Substitute for 
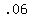and for 
:
Your teacher may want you to write 
in
functional notation as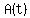 
. Ask your teacher.
-------------------
c) Find the balance after 10 years
Substitute 
for 
in
.
--------
d) Find the doubling time.
For $8000 to double, it must become $16000,
So we substitute $16000 for A and solve for t
Divide both sides by 8000
Take natural logs of both sides:
Use fact that
Divide both sides by .06:
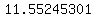or a little over 
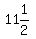years.
Edwin
