Question 158543: Solve the system by graphing.
3x-2y=4
-6x+4y=7
Found 2 solutions by gonzo, Electrified_Levi:
Answer by gonzo(654)   (Show Source): (Show Source):
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help
.
Solve the system by graphing.


.
Points are given as (x,y), to find points on both of these lines, you just replace "x" with any number and solve for "y"
.
Lets find some points on the first line
.
 , (we can use any number for "x", then we solve for "y" , (we can use any number for "x", then we solve for "y"
.
Lets replace "x" with "2",  = =  = = 
.
We will move (-2y) over to the right side
.
 = =  = =  , we will move "4" to the left side , we will move "4" to the left side
.
 = =  = =  = = 
.
To get "y", we will divide each side by "2"
.
 = =  = =  , ,
.
"x" = 2
"y" = 1
.
Since points are given as (x,y), this point would be (2,1)
.
(2,1) is a point of the line(We can check by replacing "x" with "2", "y" with "1",  = =  = =  = =  (True) (True)
.

.
Lets find another point,
.
Lets replace "x" with "0"
.
 = =  = =  = = 
.
We can multiply each side by (-1) to get (-2y) positive
.
 = =  = =  , to find "y" we will divide each side by "2" , to find "y" we will divide each side by "2"
.
 = =  = = 
.
"x" = 0
"y" = (-2)
.
Another point on the line is (0,-2)(x,y)(we can check by replacing "x" with "0", "y" with (-2),  = =  = =  = =  (True) (True)
.

.
Another point on the line is (-4,-8), We can check by replacing "x" with (-4), "y" with (-8),  = =  = =  = =  (True) (True)
.

.
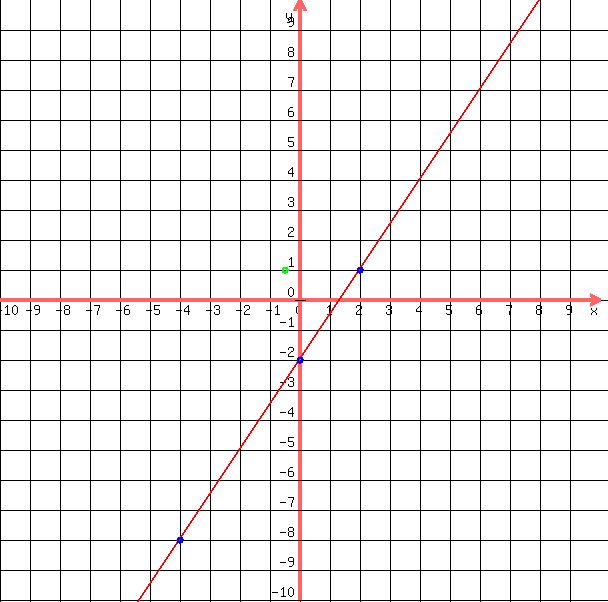
Lets draw a line through the points,
.

.
Now lets find some points for the second equation, 
.
Lets replace "x" with 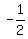 , ,  = =  = = 
.
"4y" has to equal "4", so  , divide each side by "4", , divide each side by "4",  = =  = = 
.
x = 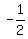
y = 1
.
One point on the line is (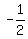 ,1 )(We can check by replacing "x" with ,1 )(We can check by replacing "x" with 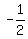 ,"y" with "1", ,"y" with "1",  = =  = =  = =  (True) (True)
.
.
Replace "x" with "4",  = =  = = 
.
"4y" will have to equal "31",  , dividing each side by "4" will get "y" , dividing each side by "4" will get "y"
.
 = =  = = 
.
x = 4
y = 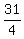 , or 7 , or 7 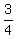
.
The point is (4,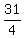 ), (we can check by replacing "x" with "4", "y" with ), (we can check by replacing "x" with "4", "y" with 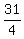 , ,  = =  = =  = =  (True) (True)
.

.
Another point on the line is ( 0, 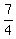 ), ( we can check by replacing "x" with "0", "y" with " ), ( we can check by replacing "x" with "0", "y" with "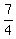 ", ",  = =  = =  = =  (True) (True)
.

.
Lets draw a line through the points
.

.
These lines are parallel, they don't have any points that intersect each other, there is no solution to the system of equations
.
Hope I helped, Levi
|
|
|