Question 141088: 3x+4y=17
6y-2x=-20
Im stuck.
Found 2 solutions by jim_thompson5910, rapaljer:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Start with the second equation Start with the second equation
 Rearrange the terms Rearrange the terms
So now we have the system of equations:

Let's use elimination to solve this system
Now in order to solve this system by using elimination/addition, we need to solve (or isolate) one variable. I'm going to solve for y.
In order to solve for one variable, we must eliminate the other variable. So if we wanted to solve for  , we would have to eliminate , we would have to eliminate  (or vice versa). (or vice versa).
So lets eliminate  . In order to do that, we need to have both . In order to do that, we need to have both  coefficients that are equal in magnitude but have opposite signs (for instance 2 and -2 are equal in magnitude but have opposite signs). This way they will add to zero. By adding to zero, they can be eliminated. coefficients that are equal in magnitude but have opposite signs (for instance 2 and -2 are equal in magnitude but have opposite signs). This way they will add to zero. By adding to zero, they can be eliminated.
So to make the  coefficients equal in magnitude but opposite in sign, we need to multiply both coefficients equal in magnitude but opposite in sign, we need to multiply both  coefficients by some number to get them to an common number. So if we wanted to get coefficients by some number to get them to an common number. So if we wanted to get  and and  to some equal number, we could try to get them to the LCM. to some equal number, we could try to get them to the LCM.
Since the LCM of  and and  is is  , we need to multiply both sides of the top equation by , we need to multiply both sides of the top equation by  and multiply both sides of the bottom equation by and multiply both sides of the bottom equation by  like this: like this:
 Multiply the top equation (both sides) by Multiply the top equation (both sides) by 
 Multiply the bottom equation (both sides) by Multiply the bottom equation (both sides) by 
Distribute and multiply


Now add the equations together. In order to add 2 equations, group like terms and combine them

Combine like terms and simplify
 Notice how the x terms cancel out Notice how the x terms cancel out
 Simplify Simplify
 Divide both sides by Divide both sides by 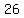 to isolate y to isolate y
 Reduce Reduce
Now plug this answer into the top equation  to solve for x to solve for x
 Start with the first equation Start with the first equation
 Plug in Plug in 
 Multiply Multiply
 Add 4 to both sides Add 4 to both sides
 Combine like terms on the right side Combine like terms on the right side
 Divide both sides by 3 to isolate x Divide both sides by 3 to isolate x
 Divide Divide
So our answer is
 and and 
which also looks like )
Now let's graph the two equations (if you need help with graphing, check out this solver)
From the graph, we can see that the two equations intersect at ) . This visually verifies our answer. . This visually verifies our answer.
 graph of graph of  (red) and (red) and  (green) and the intersection of the lines (blue circle). (green) and the intersection of the lines (blue circle).
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3x+4y=17
6y-2x=-20
Rewrite this as
3x+4y=17
-2x + 6y=-20
To eliminate the x terms, you need to find a "common number" between the x coefficients. This would be 6. Multiply both sides of the first equation by 2 and the second equation by 3, and the x terms will subtract out!
2(3x+4y)=2(17)
3(-2x + 6y)=3(-20)
6x+8y=34
-6x +18y = -60
26y = -26
y=-1
Solve for x by substituting the value of y =-1 into the first equation:
3x+4y=17
3x+4(-1) = 17
3x -4=17
3x=21
x=7
Check by substituting both values into the second equation:
-2x + 6y=-20
-2(7) + 6(-1) =-20
-14-6=-20
This checks!!
For additional explanation on the topic of Systems of Equatiaons, see my own website by clicking on my tutor name "rapaljer" anywhere in algebra.com. Take the second link on my homepage which is "Basic, Intermediate, and College Algebra: One Step at a Time", click on "Basic Algebra" and look for Chapter 4, Section 4.07. This is an explanation written for folks who didn't get math the first time!!
R^2
|
|
|