Question 123102: Please help me?
Solve 2/5x - 6 = 12
Solve by addition 5x - 3y = 13
4x - 3y = 11
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! First problem
.
Given the following equation to solve:
.

.
You don't have to do this first, but one of the things you can do to simplify this problem is
to get rid of the denominator 5 by multiplying both sides of the equation (all terms) by 5.
When you do that multiplication of the first term on the left side, the multiplier 5 cancels with
the 5 in the denominator and you are left with just 2x for the first term. When you multiply
the -6 by 5 you get -30, and, on the other side, when you multiply the 12 by 5 you get +60.
This means that you have converted the given equation to an equivalent form of:
.

.
Next, the goal is to get the term containing x on one side of the equation and everything else
on the other side. You can do this by getting rid of the -30 on the left side by adding +30 to
both sides of the equation. On the left side the addition of +30 cancels the the term -30 out.
On the right side the addition of +30 to the +60 results in +90 and the equation is then:
.

.
Solve for x by dividing both sides by the multiplier of the x (that is, divide both sides
by 2) and you get:
.

.
So the answer is x = 45.
.
You can check this answer by returning to the original equation you were given and substituting
45 for x to see if the equation balances (are both sides equal). The original equations was:
.

.
Substitute 45 for x and you have:
.

.
One-fifth of 45 is 9 so two-fifths of 45 is 18. Substitute 18 for 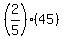 and and
you get:
.

.
which reduces to  and the equation balances ... so the answer of x = 45 is correct. and the equation balances ... so the answer of x = 45 is correct.
.
Second problem:
.
Given the two equations:
.
+5x - 3y = +13
+4x - 3y = +11
.
To solve these by addition, the object is to get one of the terms in the top equation to
be equal to but of opposite in sign to the corresponding term in the bottom equation.
.
Notice that both of the equations have a term -3y in them. But they both have the same sign.
Suppose that we multiplied the bottom equation by -1 (multiply all terms on both sides). If
we did that our pair of equations would then be:
.
+5x - 3y = +13
-4x + 3y = -11
.
Now if we add the two equations vertically (in columns) the sum of the x-terms is 5x - 4x = x.
The two y-terms are equal but of opposite signs so when you add them they cancel out and disappear.
And on the right side the +13 and -11 add to give +2. So the sum of the two equations leaves
you with:
.
+x = +2
.
To solve for y, just return to either one of the original equations and substitute 2 for x
and solve for y. Let's return to the original top equation of:
.
+5x - 3y = +13
.
Substitute 2 for x and this equation becomes:
.
5*2 - 3y = +13
.
Doing the multiplication 5*2 simplifies this equation to:
.
10 - 3y = 13
.
Get rid of the 10 on the left side by subtracting 10 from both sides to get:
.
-3y = 3
.
Solve for y by dividing both sides of the equation by -3 and you have:
.
y = 3/(-3) = -1
.
So the common solution we have for the set of equations is x = 2, y = -1
.
Let's check this by going to the bottom equation of the original pair of equations and
substituting 2 for x and -1 for y to see if the equation balances. The original bottom equation
was:
.
+4x - 3y = +11
.
Making the substitutions for x and y results in:
.
4*2 - 3(-1) = 11
.
Multiplying out the two terms on the left side gives:
.
8 + 3 = 11
.
This reduces to 11 = 11 which indicates that our answers of x = 2 and y = -1 are correct.
.
Hope this helps to increase your understanding of these two problems.
.
|
|
|