SOLUTION: For certain values of k and m, the system a + 2b = -3 4a + 2b = k - 2a - mb + 6a + 2b + 5 has infinitely many solutions (a,b). What are k and m?

Simplify second equation by combining common terms.


You will get an equivalent equation

    0 = k - mb + 5.    (*)


If m =/= 0, then this equation has a unique solution for "b"

    b = .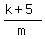


You then substitute this expression for "b" into the first equation and get a unique solution for "a".


So, if m =/= 0,  you always has the unique solution to the system of equations.


The only case, when you have infinitely many solutions for "b", is the case m= 0.

Then k must be -5 , according to equation (*).


In this way, you get the 


ANSWER.  For  m= 0  and k= -5, the given system has infinitely many solutions.

         Conversely, in order for the given system has infinitely many solutions, "m" must be zero and "k"  must be -5.

         Thus the necessary and sufficient condition for the given system to have infinitely many solutions
         is the condition m= 0, k= -5.