Question 1204620: The hot water tap can fill the tub in 10 minutes. The cold water tap can fill the tub in 8 minutes. How long would it take to fill the tub if both taps are opened?
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Let's say the tub has a capacity of 10*8 = 80 gallons.
The capacity doesn't matter. You can pick any number you want. I'm picking this value so the unit rates are whole numbers.
The hot water fills the tub in 10 minutes, so its unit rate is 80/10 = 8 gallons per minute
The formula I used was: rate = (amount done)/(time)
I'm assuming that the cold water tap isn't on.
The cold water tap can fill the tub in 8 minutes, to give it a unit rate of 80/8 = 10 gallons per minute.
I'm assuming that the hot water tap isn't on.
The combined unit rate of both hot and cold is 8+10 = 18 gallons per min.
The goal is to fill the 80 gallon tub and we can do so at a combined rate of 18 gallons per minute.
time = (amount done)/(rate)
time = 80/18
time = 4.44 minutes approximately
An alternative, and perhaps the standard textbook way to solve rates problems like this, is to solve the equation  , but this method may be a bit cryptic and not that intuitive (in my opinion).
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
This kind of "working together" problem, with two workers working at different rates, is so common that it might be useful to learn the short answer:
If two workers alone take A hours and B hours to complete a job, then the number of hours it takes them to do the job together is  .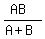
Of course the unit of time is not relevant -- it could be minutes, or years, or milliseconds....
So for this problem the quick answer is 80/18 = 40/9 minutes.
For another easy way to solve this kind of problem, consider the least common multiple of the two given times. For this problem, with the two times being 10 and 8 minutes, the least common multiple is 40 minutes.
Now consider the amount of work the two taps could do in 40 minutes. The hot water tap could fill the tub 40/10 = 4 times; the cold water tap could fill the tub 40/8 = 5 times.
So in 40 minutes the two taps together could fill the tub 4+5 = 9 times; so the number of minutes it takes them together to fill the one tub is 40/9.
ANSWER: 40/9 minutes
|
|
|
