Question 118448This question is from textbook structure and method book 1
: I AM WORKING ON THE aMERICAN SCHOOL CIRICULUM AND I AM DOING A HOME TEST. I HAVE THE FOLLOWING WORD PROBLEM AND I CAN'T UNDERSTAND HOW TO GET THE TWO ANSWERS ASKED FOR.
A SAILBOAT TRAVELS 20 MILES DOWNSTREAM IN 3 HOURS.IT RETURNS IN 4 HOURS.FIND THE SPEED OF THE SAILBOAT IN STILL WATERAND THE RATE OF THE CURRENT.
I CAN FIGURE OUT THAT THE RATE OF THE BOAT GOING DOWN STREAM WOULD TRAVEL 6.23 MPH AND COMMING BACK IT WOULD TRAVEL 5 MPH. I CAN'T FIGURE OUT HOW THAT WILL HELP ME.
This question is from textbook structure and method book 1
Found 2 solutions by solver91311, ankor@dixie-net.com:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Calculating the downstream and upstream rates was a good start, except that you made a slight arithmetic error in calculating the downstream rate --  approximately, not 6.23. approximately, not 6.23.
Before we do anything else, we need to make a couple of assumptions. Since this is a sailboat, the boat speed through still water is a function of the wind speed and direction, so let's assume that the wind speed remained constant for the entire trip and the wind direction was at 90 degrees to the direction of travel. That eliminates any variables due to the wind. Second we have to assume that the rate of the current was constant for the entire trip.
But let's look at the problem a little differently. We know that  where d is distance, r is rate, and t is time. What we need to deal with is two different rates: One is the rate of the boat through still water, and the other is the rate of the current. When the boat is travelling downstream, the rate of the current ADDS to the overall speed of the boat, and when traveling upstream the current SUBTRACTS from the overall speed. where d is distance, r is rate, and t is time. What we need to deal with is two different rates: One is the rate of the boat through still water, and the other is the rate of the current. When the boat is travelling downstream, the rate of the current ADDS to the overall speed of the boat, and when traveling upstream the current SUBTRACTS from the overall speed.
Let's say the rate of the boat through still water is 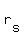 and the rate of the current is and the rate of the current is 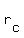 . The distance traveled in either direction is 20 miles, so we can write: . The distance traveled in either direction is 20 miles, so we can write:
 for the downstream trip, and for the downstream trip, and
 for the upstream trip. for the upstream trip.
Divide both sides of the first equation by 3 (leaving the left side result in improper fraction form for the time being), and both sides of the second equation by 4.


Now, add these two equations term by term:
 , and simplify: , and simplify:

 , and now we know the speed of the boat through still water, i.e. 5 and 5/6 or roughly 5.83 mph. , and now we know the speed of the boat through still water, i.e. 5 and 5/6 or roughly 5.83 mph.
Using this value, we can substitute in either of the original equations to solve for the rate of the current.


 , and now we know the speed of the current, i.e. 5/6 or roughly 0.83 mph. , and now we know the speed of the current, i.e. 5/6 or roughly 0.83 mph.
Let's check the answer.
If the boat goes 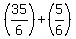 mph downstream, then using mph downstream, then using  or or  , should give us 3 hours. I'll let you do the arithmetic. , should give us 3 hours. I'll let you do the arithmetic.
If the boat goes 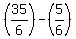 mph upstream, mph upstream,  should give us 4 hours. Again, you get to do the arithmetic. should give us 4 hours. Again, you get to do the arithmetic.
Hope that helps,
John
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A SAILBOAT TRAVELS 20 MILES DOWNSTREAM IN 3 HOURS.IT RETURNS IN 4 HOURS. FIND THE SPEED OF THE SAILBOAT IN STILL WATER AND THE RATE OF THE CURRENT.
I CAN FIGURE OUT THAT THE RATE OF THE BOAT GOING DOWN STREAM WOULD TRAVEL 6.23 MPH AND COMING BACK IT WOULD TRAVEL 5 MPH.
:
One way is to use two unknowns and use the elimination method
:
Let x = speed of the boat in still water
Let y = speed of the current
then:
(x+y) = speed downstream
(x-y) = speed upstream
:
Write two distance equations: Distance = speed * time
Down stream: 3(x+y) = 20
Upstream: 4(x-y) = 20
:
3x + 3y = 20
4x - 4y = 20
:
Multiply the 1st equation by 4 and the 2nd equation by 3
12x + 12y = 80
12x - 12y = 60
---------------adding eliminates y, find x
24x + 0y = 140
x = 140/24
x = 5.83 mph speed of the boat in still water
:
Find y
3(5.833) + 3y = 20
17.5 + 3y = 20
3y = 20 - 17.5
3y = 2.5
y = 2.5/3
y = .833 mph is the speed of the current
:
:
Check solutions in the 2nd equation
4(5.833) - 4(.833) =
23.33 - 3.33 = 20 confirms our solution
|
|
|