Question 1184453: Suppose A is a 3x2 matrix, B is a pxq and C is a 5x4 matrix. If ABC is defined, then what are p and q?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Every matrix has a "DOWN" dimension and an "ACROSS" dimension. This matrix,
for example, where the #'s represent numbers (called "elements"):
 has a "DOWN" dimension of 3, and an "ACROSS" dimension of 5. Its dimensions
are always taken "DOWN" by "ACROSS", or 3x5. This matrix:
has a "DOWN" dimension of 3, and an "ACROSS" dimension of 5. Its dimensions
are always taken "DOWN" by "ACROSS", or 3x5. This matrix:
 has a "DOWN" dimension of 5, and an "ACROSS" dimension of 3. Its dimensions
are "DOWN" by "ACROSS", or 5x3.
In order to multiply a matrix on the left by a matrix on its immediate
right, the "ACROSS" dimension for the matrix on the left MUST be the same as
the "DOWN" dimension of the matrix on its immediate right. Otherwise, their
multiplication is not defined.
---------------------------------------------
>>>Suppose A is a 3x2 matrix, B is a pxq and C is a 5x4 matrix. If ABC is
defined, then what are p and q?
So
has a "DOWN" dimension of 5, and an "ACROSS" dimension of 3. Its dimensions
are "DOWN" by "ACROSS", or 5x3.
In order to multiply a matrix on the left by a matrix on its immediate
right, the "ACROSS" dimension for the matrix on the left MUST be the same as
the "DOWN" dimension of the matrix on its immediate right. Otherwise, their
multiplication is not defined.
---------------------------------------------
>>>Suppose A is a 3x2 matrix, B is a pxq and C is a 5x4 matrix. If ABC is
defined, then what are p and q?
So   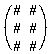 and and
   with a DOWN dimension of 3 and an ACROSS dimension of 2.
So in order to be able to multiply A on the left by B on its right, the
ACROSS number of A must be the same as the DOWN dimension of B, so p, the
DOWN dimension of B must be 2. So p = 2.
Now in order to multiply B on the left by C on its right, the ACROSS
dimension of B must equal the DOWN dimension of C, which is 5. So q, the
ACROSS dimension of B must equal the DOWN dimension of C, so q=5.
So the dimensions of B must be pxq which are 2x5:
So for ABC to be defined, we must have this sort of thing:
with a DOWN dimension of 3 and an ACROSS dimension of 2.
So in order to be able to multiply A on the left by B on its right, the
ACROSS number of A must be the same as the DOWN dimension of B, so p, the
DOWN dimension of B must be 2. So p = 2.
Now in order to multiply B on the left by C on its right, the ACROSS
dimension of B must equal the DOWN dimension of C, which is 5. So q, the
ACROSS dimension of B must equal the DOWN dimension of C, so q=5.
So the dimensions of B must be pxq which are 2x5:
So for ABC to be defined, we must have this sort of thing:
  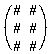   Notice again, that the ACROSS dimension of each matrix on the left must
always equal to the DOWN dimension of the matrix next to it on the right.
Edwin
Notice again, that the ACROSS dimension of each matrix on the left must
always equal to the DOWN dimension of the matrix next to it on the right.
Edwin
|
|
|