SOLUTION: A train leaves Station X and travels east at 30 km/h. Two hours later, another train leaves the same station and travels in the same direction on a parallel tract at 45 km/h. At wh

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: A train leaves Station X and travels east at 30 km/h. Two hours later, another train leaves the same station and travels in the same direction on a parallel tract at 45 km/h. At wh      Log On


   

Question 1171125: A train leaves Station X and travels east at 30 km/h. Two hours later, another train leaves the same station and travels in the same direction on a parallel tract at 45 km/h. At what point will the faster train overtake the slower train?

Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let d be the distance from the starting point to the overtaking point 
(exactly the unknown value under the question).


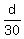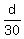For the first train, the travel time is  d%2F30  hours.

For the second train, the travel time is  d%2F45  hours.


The difference is 2 hours, according to the condition


    d%2F30 - d%2F45 = 2  hours.


You got your basic equation to find the unknown distance d.


To solve the equation, multiply both sides by 90.  You will get


    3d - 2d = 180

       d    = 180.


ANSWER.  The overtaking point is in 180 miles from the station X.

Solved.