Question 1161245: Use the slope and y-intercept to graph the following system of equations. State the solution to the system of equations. y = 1/2x - 6 and -2x - y = -9.
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  .........eq.1->already in slope intercept form .........eq.1->already in slope intercept form
 .............eq.2 .............eq.2
---------------------------------------------
 .............eq.2, write in slope intercept form .............eq.2, write in slope intercept form
 ...........eq.2 ...........eq.2
---------------------------------------
 .........eq.1, slope is .........eq.1, slope is  , y-intercept is ( , y-intercept is ( , , ) )
 ...........eq.2, slope is ...........eq.2, slope is  , y-intercept is ( , y-intercept is ( , , ) )
since a slope of eq.2 is negative reciprocal of slope of the eq.1, lines are 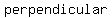 to each other to each other
for each line find one more point to graph them
 ...let ...let 



 -> x-intercept is at ( -> x-intercept is at ( , , ) )
 ....let ....let 



 -> x-intercept is at ( -> x-intercept is at ( , , ) )
graph the line  using points ( using points ( , , ) and ( ) and ( , , ) )
and
graph the line  using points ( using points ( , , ) and ( ) and ( , , ) )

as you can see from the graph, intersection point is at ( , , ), therefore solution to the system of equations is: ), therefore solution to the system of equations is:


Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
First get it in the form y = mx + b if it's not already in that form.
 That's already in the form y = mx + b,
The "b", which reminds us of the word "begin" is -6.
That tells us where to begin on the y-axis:
So we put our pencil at -6 on the y-axis, where the
dot is below
That's already in the form y = mx + b,
The "b", which reminds us of the word "begin" is -6.
That tells us where to begin on the y-axis:
So we put our pencil at -6 on the y-axis, where the
dot is below
 The "m", which reminds us of the word "move" is 1/2, which is the slope.
Its numerator tells us how many units to go up or down. If it's a
psitive number, numerator tells us how many its to go up, and if it's
a negative number it tells us how many units to go down. Since 1/2 is
a positive number, we go up the numerator number of units, which is up
1 unit, so we draw a line from that point we drew upward 1 unit. See the
green line drawn upward 1 unit below
The "m", which reminds us of the word "move" is 1/2, which is the slope.
Its numerator tells us how many units to go up or down. If it's a
psitive number, numerator tells us how many its to go up, and if it's
a negative number it tells us how many units to go down. Since 1/2 is
a positive number, we go up the numerator number of units, which is up
1 unit, so we draw a line from that point we drew upward 1 unit. See the
green line drawn upward 1 unit below
 The denominator tells us how many units to go right. We ALWAYS go right
with the denominator. The denominator of m is 2 so we go right the
denominator number of units, so we draw a line from that point we drew
rightward 2 units. See the horizontal green line drawn rightward 2 units
below:
The denominator tells us how many units to go right. We ALWAYS go right
with the denominator. The denominator of m is 2 so we go right the
denominator number of units, so we draw a line from that point we drew
rightward 2 units. See the horizontal green line drawn rightward 2 units
below:
 Now take a ruler and draw the line which the equation represents. The
line goes through the first point we drew and goes through the end point
of the green horizontal line. Like this:
Now take a ruler and draw the line which the equation represents. The
line goes through the first point we drew and goes through the end point
of the green horizontal line. Like this:
 But the second one, -2x - y = -9, is not in the form y = mx + b
Here is how we get it in that form:
-2x - y = - 9
+2x +2x
-------------------
-y = 2x - 9
Divide every term by -1
-y = 2x - 9
——— —— ———
-1 -1 -1
y = -2x + 9
Now we have to consider m=-2 as the fraction m=-2/1
---
The "b", which reminds us of the word "begin" is 9.
That tells us where to begin on the y-axis:
So we put our pencil at 9 on the y-axis, where the
dot is below
But the second one, -2x - y = -9, is not in the form y = mx + b
Here is how we get it in that form:
-2x - y = - 9
+2x +2x
-------------------
-y = 2x - 9
Divide every term by -1
-y = 2x - 9
——— —— ———
-1 -1 -1
y = -2x + 9
Now we have to consider m=-2 as the fraction m=-2/1
---
The "b", which reminds us of the word "begin" is 9.
That tells us where to begin on the y-axis:
So we put our pencil at 9 on the y-axis, where the
dot is below
 The "m", which reminds us of the word "move" is -2/1, which is the slope.
Its numerator tells us how many units to go up or down. If it's a
positive number, numerator tells us how many its to go up, and if it's
a negative number it tells us how many units to go down. Since -2/1 is
a negative number, we go down the numerator number of units, which is down
2 units, so we draw a line from that point we drew downward 2 units. See the
green line drawn downward 2 units below:
The "m", which reminds us of the word "move" is -2/1, which is the slope.
Its numerator tells us how many units to go up or down. If it's a
positive number, numerator tells us how many its to go up, and if it's
a negative number it tells us how many units to go down. Since -2/1 is
a negative number, we go down the numerator number of units, which is down
2 units, so we draw a line from that point we drew downward 2 units. See the
green line drawn downward 2 units below:
 The denominator tells us how many units to go right. We ALWAYS go right
with the denominator. The denominator of m is 1 so we go right the
denominator number of units, so we draw a line from that point we drew
rightward 1 units. See the horizontal green line drawn rightward 1 units
below:
The denominator tells us how many units to go right. We ALWAYS go right
with the denominator. The denominator of m is 1 so we go right the
denominator number of units, so we draw a line from that point we drew
rightward 1 units. See the horizontal green line drawn rightward 1 units
below:
 Now take a ruler and draw the line which the equation represents. The
line goes through the first point we drew and goes through the end point
of the green horizontal line. Like this:
Now take a ruler and draw the line which the equation represents. The
line goes through the first point we drew and goes through the end point
of the green horizontal line. Like this:
 Edwin
Edwin
|
|
|