Question 1157597: Town A and Town B were located close to each other, and recently merged into one city. Town A had a population with 12% African Americans. Town B had a population with 8% African Americans. After the merge, the new city has a total of 4000 residents, with 9.4% African Americans. How many residents did Town A and Town B used to have?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52783)   (Show Source):
You can put this solution on YOUR website! .
a + b = 4000 (1)
0.12a + 0.08b = 0.094*4000 (2)
From equation (1), express a = 4000 - b ans substitute it into equation (2), replacing "a" there
0.12*(4000-b) + 0.08b = 0.094*4000.
Now b = 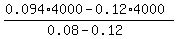 = 2600.
ANSWER. Population B is 2600 residents; population A is the rest 4000-2600 = 1400 residents.
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is a non-algebraic method for solving this type of "mixture" problem.
The difference between 8% and 9.4% is 1.4%; the difference between 12% and 9.4% is 2.6%.
That means the ratio of the populations of the two towns before the merger was 1.4:2.6, or 14:26.
With a combined population of 40,000, and a ratio of 14:26, the populations of the two towns were 14,000 and 26,000.
And since 9.4% is closer to 8% than to 12%, town B had the larger population.
ANSWERS:
Town A: 14,000
Town B: 26,000
CHECK:
.12(14,000) + .08(26,000) = 1680+2080 = 3760
.094(40,000) = 3760
|
|
|
