Question 1154912: You have $144 in one-, five-, and ten-dollar bills. There are 35 bills in total, and two more ten-dollar bills than five-dollar bills. How many bills of each type are there?
Found 3 solutions by Theo, ikleyn, josgarithmetic:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! let x = the number of 1 dollar bills and y = the number of 5 dollar bills and z = the number of 10 dollar bills.
you get:
x + y + z = 35
x + 5y + 10z = 144
since you have 2 more 10 dollar bills than 5 dollar bills, you get:
z = y + 2
replace z with y + 2 in the first 2 equations to get:
x + y + y + 2 = 35
x + 5y + 10 * (y + 2) = 144
simplify both equations to get:
x + 2y + 2 = 33
x + 5y + 10y + 20 = 144
subtract the constants on the left side of the equation from both sides of the equation and simplify further to get:
x + 2y = 33
x + 15y = 124
subtract the first equation from the first to get:
13y = 91
solve for y to get:
y = 91 / 13 = 7
since z = y + 2, then z = 9
first original equation becomes:
x + 7 + 9 = 35
solve for x to get x = 35 - 16 = 19
you have:
x = 19
y = 7
z = 9
second original equation becomes:
19 * 1 + 7 * 5 + 9 * 10 = 19 + 35 + 90 = 144
both original equations are true when x = 19 and y = 7 and z = 9
you have 19 one dollar bills and 7 five dollar bills and 9 ten dollar bills.
that's your solution.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
I will make you surprised.
I will solve the problem using only one single unknown.
Watch my steps (!)
Let x be the number of the 5-dollar bills.
Then the number of the 10-dollar bills is (x+2), according to the condition.
Next, the one-dollar bills are the rest (35 - x - (x+2)) = 33 - 2x banknotes.
Now, I write the total money equation
1*(33-2x) + 5x + 10*(x+2) = 144.
Next, I simplify it
33 - 2x + 5x + 10x + 20 = 144
-2x + 5x + 10x = 144 - 33 - 20
13x = 91
x = 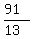 = 7.
ANSWER. 7 (seven) 5-dollar bills; 7+2 = 9 10-dollar bills and the rest 35 - 7 - 9 = 19 one-dollar bills.
CHECK. 7*5 + 9*10 + 19*1 = 144. ! Precisely correct !
Solved.
----------------
This problem, and many hundreds similar problems, are designed, are destined and are expected to be solved
by 6-7 grade students, who don't know any systems of equations, and who need to be touched/(to be trained) on
how to solve them (the problems) using one single equation in one single unknown.
It is why such problems are/were created, at all.
To see many other similar solved problems, look into the lessons
- More complicated coin problems
- More complicated word problems to solve using a single linear equation
- Advanced word problems to solve using a single linear equation
in this site.
Answer by josgarithmetic(39617)  (Show Source):
|
|
|
