Question 1151064: Pre-orders for the year cost $38 each, while full price costs $45 each. If 24 students in Mr. Hillmans homeroom purchased yearbooks for a total of $975, how many students pre-ordered and how many bought their yearbook at full price ?
Found 3 solutions by ikleyn, rothauserc, greenestamps:
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
x at 38 dollars; (24-x) at 45 dollars.
The total money equation is
38x + 45*(24-x) = 975 dollars.
From the equation, express "x" and calculate
x = 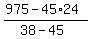 = 15.
ANSWER. 15 at 38 dollars and the rest, 24-15 = 9 at 45 dollars.
CHECK. 15*38 + 9*45 = 975 dollars. ! Precisely correct !
Solved.
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! let x be the number of pre-orders and y be the number of regualar orders
:
(1) x + y = 24
:
(2) 38x +45y = 975
:
solve equation 1 for x and substitute for x in equation 2
:
x = 24 - y
:
38(24 - y) + 45y = 975
:
912 -38y +45y = 975
:
7y = 63
:
y = 9
:
x = 24 - 9 = 15
:
*****************************************************
There are 15 pre-orders and 9 regular orders
:
check answer with equation 2
:
38(15) +45(9) = 975
:
570 +405 = 975
:
975 = 975
:
answer checks
****************************************************
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is a quick way to solve this problem and many similar problems without algebra -- if, of course, an algebraic solution is not required.
(1) If all 24 students had purchased the yearbooks with pre-orders, the total cost would have been 24 times $38, or $912. That is $975-$912 = $63 less than the actual total.
(2) Each full price order costs $45-$38 = $7 more than a pre-order.
(3) The number of full price orders required to make up the additional $63 is $63/$7 = 9.
ANSWER: 9 students paid full price; so 24-9=15 students bought the yearbooks with pre-orders.
|
|
|
