SOLUTION: It's 207.5 miles from Amberwood to Bravotown. It's another 220 miles from Bravotown to C-town. Ethan drives 30 miles faster from Bravotown to C-town than from Amberwood to Bravotow

Let x be the average rate from A to B, in miles per hour. 

Then the average rate from B to C is  (x+30) mph.



The traveling time from A to B is 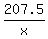  hours;

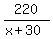The traveling time from B to C is   hours.



The total time is 12.3 hours, which gives you an equation


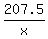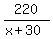     +   = 12.3  hours.


It is the "time" equation, and as soon as you get it, the setup is just completed.



To solve the equation, multiply both sides by x*(x+30)*10.  You will get


    2075*(x+30) + 2200*x = 123x*(x+1)


Simplify this quadratic equation and write it in the standard form


Then solve it and find its positive root.


It will be the answer for the average speed from A to B.


The average speed from B to C is 30 mph greater.