Question 1142961: A number is 1 more than twice another. Their squares differ by 176. What is the smaller number?
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the "another" number ; then "a number" is (2x+1).
From the condition, you have ONE OF THE TWO equations
x^2 - (2x+1)^2 = 176, (1)
or
(2x+1)^2 - x^2 = 176. (2)
Equation (1) implies
x^2 - 4x^2 - 4x - 1 = 176
-3x^2 - 4x - 177 = 0,
3x^2 + 4x + 177 = 0.
It has no real solutions. It only has the solutions in the complex domain.
To find its solutions in complex numbers, use the quadratic formula.
But for complex numbers the notion "one complex number is 1 more than another" IS NOT DEFINED,
since complex numbers do not form an ordered set (!)
So, based on common sense, we should not consider this case.
Equation (2) implies
4x^2 + 4x + 1 - x^2 = 176
3x^2 + 4x - 175 = 0
Its real roots are
 = = 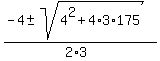 = = 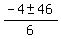
 = =  = =  = 7, and = 7, and
 = = 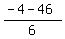 = = 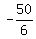 = =   .
ANSWER. There are two pairs of numbers satisfying the condition.
One pair is (7, 2*7+1) = (7,15) with the smaller number 7.
The other pair is ( .
ANSWER. There are two pairs of numbers satisfying the condition.
One pair is (7, 2*7+1) = (7,15) with the smaller number 7.
The other pair is (  , ,  ) with the smaller number ) with the smaller number   . .
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! A number is 1 more than twice another. Their squares differ by 176. What is the smaller number?
Considering that these are INTEGERS, 
If not, 
|
|
|