SOLUTION: Use substitution to solve the system. (Simplify your answer completely. If the system is dependent, enter a general solution in terms of x and y. If there is no solution, enter NO

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: Use substitution to solve the system. (Simplify your answer completely. If the system is dependent, enter a general solution in terms of x and y. If there is no solution, enter NO       Log On


   

Question 1130672: Use substitution to solve the system. (Simplify your answer completely. If the system is dependent, enter a general solution in terms of x and y. If there is no solution, enter NO SOLUTION.)
3y + x = 1
y= -1/3 x + 1/3
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

3y+%2B+x+=+1
y=+-%281%2F3%29+x+%2B+1%2F3
------------------------
x+%2B+3y=+1
%281%2F3%29+x%2By=+1%2F3

Solved by pluggable solver: Solving a linear system of equations by subsitution


%281%2F3%29%2Ax%2B%281%29%2Ay=1%2F3 Start with the second equation


3%28%281%2F3%29%2Ax%2B%281%29%2Ay%29=%283%29%2A%281%2F3%29 Multiply both sides by the LCD 3



1%2Ax%2B3%2Ay=1 Distribute and simplify


-----------------------------------------



Lets start with the given system of linear equations

1%2Ax%2B3%2Ay=1
1%2Ax%2B3%2Ay=1

Now in order to solve this system by using substitution, we need to solve (or isolate) one variable. I'm going to choose y.

Solve for y for the first equation

3%2Ay=1-1%2AxSubtract 1%2Ax from both sides

y=%281-1%2Ax%29%2F3 Divide both sides by 3.


Which breaks down and reduces to



y=1%2F3-%281%2F3%29%2Ax Now we've fully isolated y

Since y equals 1%2F3-%281%2F3%29%2Ax we can substitute the expression 1%2F3-%281%2F3%29%2Ax into y of the 2nd equation. This will eliminate y so we can solve for x.


1%2Ax%2B3%2Ahighlight%28%281%2F3-%281%2F3%29%2Ax%29%29=1 Replace y with 1%2F3-%281%2F3%29%2Ax. Since this eliminates y, we can now solve for x.

1%2Ax%2B3%2A%281%2F3%29%2B3%28-1%2F3%29x=1 Distribute 3 to 1%2F3-%281%2F3%29%2Ax

1%2Ax%2B3%2F3-%283%2F3%29%2Ax=1 Multiply



1%2Ax%2B1-1%2Ax=1 Reduce any fractions

1%2Ax-1%2Ax=1-1 Subtract 1 from both sides


1%2Ax-1%2Ax=0 Combine the terms on the right side



0%2Ax=0 Now combine the terms on the left side.
0=0 Since this expression is true for any x, we have an identity.


So there are an infinite number solutions. The simple reason is the 2 equations represent 2 lines that overlap each other. So they intersect each other at an infinite number of points.

If we graph 1%2Ax%2B3%2Ay=1 and 1%2Ax%2B3%2Ay=1 we get

+graph%28+500%2C+600%2C+-6%2C+5%2C+-10%2C+10%2C+%281-1%2Ax%29%2F3%29+ graph of 1%2Ax%2B3%2Ay=1


+graph%28+500%2C+600%2C+-6%2C+5%2C+-10%2C+10%2C+%281-1%2Ax%29%2F3+%29+ graph of 1%2Ax%2B3%2Ay=1 (hint: you may have to solve for y to graph these)

we can see that these two lines are the same. So this system is dependent

Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.

            I will do exactly as instructed. 


From the second equation, substitute this expression for y into the first equation.


You will get


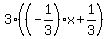    3%2A%28%28-1%2F3%29x+%2B+1%2F3%29 + x = 1


Simplify it step by step


    -x + 1 + x = 1


Cancel similar terms


    0 = 0.


Every time when you get this identity after making equivalent transformations, it means that the original equation / (system of equations) 

is, actually, an identity and has infinitely many solutions.


It means that the system is dependent.


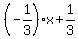The general solution is  y = %28-1%2F3%29x+%2B+1%2F3, as the second original equation states.

------------

Actually, the stiff instructions prevents any initiative from the students.

But, actually, every educated student in healthy mind should notice (after 10 seconds looking into the system) that
the two equations are, indeed, equivalent and represent the same straight line, so the system is dependent.


/\/\/\/\/\/\/\/\/\/\/\/\/

I am very surprised on how the tutor @LoverMath1 treats these problems on solving equation systems.

By applying this "pluggable solver", she turns / transforms / converts very serious educational task of teaching students
into some unreadable and nonsensical text.