Question 1110439: Jack and Jill spent two weeks touring Boston, New York City, Philadelphia, and Washington D.C. They paid $120,$200,$80, and $100 per night respectively. Their total bill was $2020. The number of days spent in NYC was the same as the sum of the days spent in Boston and D.C. They spent three times as many days in NYC as they did in Philly. How many days did they stay in each city?
a) answer question using a combination of algebra and logic.
b) answer the question again using a 4x4 system of equations.
Does this mean there's another way to do this without a system of equations? That's the only way I can think of doing it. I just know that 120B+200N+80P+100W=2020.
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Jack and Jill spent two weeks touring Boston, New York City, Philadelphia, and Washington D.C.
let b, n, p, and w = the no. of days in each season, write an equation for each statement
:
They paid $120,$200,$80, and $100 per night respectively.
Their total bill was $2020.
120b + 200n + 80p + 100w = 2020
Simplify, divide by 20
6b + 10n + 4p + 5w = 201
:
The number of days spent in NYC was the same as the sum of the days spent in Boston and D.C.
n = b + w
or
b = n - w
:
They spent three times as many days in NYC as they did in Philly.
n = 3p
or
p = 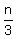
:
a) answer question using a combination of algebra and logic.
Substitute in the 1st equation, for b & p
6(n-w) + 10n + 4(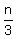 + 5w = 101 + 5w = 101
get rid of the fraction, multiply thru b 3
18(n-w) + 30n + 4n + 15w = 303
18n - 18w + 30n + 4n + 15w = 303
combine like terms
52n - 3w = 303
have 4 unknowns and only 3 equations, but we know they have to be integers
Write an equation we can enter into a graphing calc
3w = 52n - 303
w = 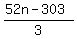
w =  n - 101 n - 101
table reveals only one integer solution that makes sense
n = 6, w = 3
therefore
p = 6/3 = 2 days
b = 6 - 3 = 3 days
:
How many days did they stay in each city?
Boston 3 days, New York 6 days, Philly 2 days and Wash 3 days
see if that works
120(3) + 200(6) + 2(80) + 100(3) = 2020
:
b) answer the question again using a 4x4 system of equations.
I don't know either, how you could do this with a 4 by 4 matrix
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The usual practice in hotels is to pay for night.
But, specially for the purpose of this problem, I will assume that they pay for each DAY and that the number of days was 14 ("two weeks" literally).
Solution
Let P be the number of days in Philly.
Then the number of days in NYC is 3P, from the condition.
We also are given that the number of days in NYC, 3P, is equal to B + W.
So we have
P + 3P + (B + W) = 14, or, replacing B + W by "3P",
P + 3P + 3P = 14,
7P = 14 ====> P =  = 2.
Answer. 2 days in P; 6 days in NYC; and remaining 14 - (2+6) = 6 days in B + W. = 2.
Answer. 2 days in P; 6 days in NYC; and remaining 14 - (2+6) = 6 days in B + W.
It is how my logic works.
Still, it is not the final solution yet, but I just reduced the problem to the only 2 (two, TWO) unknowns B and W,
and at this point, I an sure, now you are able to complete the solution WITHOUT MY HELP,
using REMAINING CONDITION on the total cost.
|
|
|