SOLUTION: The no. Of solution of (x,y,z)to the system of equations x+2y+4z=9, 4yz+2xz+xy=13,xyz=13, such that at least two of x,y,z are integers is... A)3 B)5 C)6 D)4

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: The no. Of solution of (x,y,z)to the system of equations x+2y+4z=9, 4yz+2xz+xy=13,xyz=13, such that at least two of x,y,z are integers is... A)3 B)5 C)6 D)4      Log On


   

Question 1098865: The no. Of solution of (x,y,z)to the system of equations x+2y+4z=9, 4yz+2xz+xy=13,xyz=13, such that at least two of x,y,z are integers is...
A)3
B)5
C)6
D)4
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
The system as it is posted,  HAS NO  integer or rational solutions  AT ALL.

Therefore,  the problem makes no sense.

But,  actually,  a brilliant problem is hidden behind this NONSENSE.

In order to make it VISIBLE and SOLVABLE,  I changed the condition in this way: 

    Solve the system


           x + 2y  + 4z = 9, 
        4yz + 2xz + xy = 13,
              xyz      =  3.

Notice that I changed the third equation.

Solution 

Introduce new variables 

p = x,  q = 2y  and  r = 4z.           (1)

Then  pq = 2xy,  pr = 4xz,  and  qr = 8yz,  so  pq + pr + qr = 2xy + 4xz + 8yz = 2*(xy + 2xz + 4yz).


Therefore, the original system takes the form

p + q + r = 9,          (2)    

pq + pr + qr = 26,      (3)    (26 = 2*13)

pqr = 24.               (4)    (24 = 8*3)


Thus, according to the Vieta's theorem,  p, q and r are the roots of this polynomial equation of the degree 3:

t^3 - 9t^2 + 26t  - 24 = 0.


By applying the "Rational root theorem", you can find the integer roots of this equation.

If exist, they are among the integer divisors of the constant term 24, i.e. among the number set

{+/-1, +/-2, +/-3, +/-6, +/-12, +/-24}.


Or, you can plot a graph, and it will tell you/ (will show you) what the roots are:





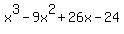Plot y = x%5E3+-+9x%5E2+%2B+26x++-+24


and the plot says that the roots are t = 2, 3 and 4.  // You can check it manually.


Thus the solution (p,q,r) to the system  (2), (3), (4)  is ANY permutation of numbers  (2,3,4).
Any of 3! = 1*2*3 = 6 possible permutations.

Now we must return from variables p, q and r to the original variables x, y and z using formulas (1).

Since the original system is EQUIVALENT to the system (2), (3), (4) due to substitution (1),

it implies that the following values (triples) of x, y and z are the solutions to the original system:

    1)  (p,q,r) = (2,3,4)  ====> x= 2,  y= 3/2,  z=  1;

    2)  (p,q,r) = (4,2,3)  ====> x= 4,  y= 1,    z= 3/4;

    3)  (p,q,r) = (3,4,2)  ====> x= 3,  y= 2,    z= 1/2;
 
    4)  (p,q,r) = (3,2,4)  ====> x= 3,  y= 1,    z=  1;  

    5)  (p,q,r) = (4,3,2)  ====> x= 4,  y= 3/2,  z= 1/2;

    6)  (p,q,r) = (2,4,3)  ====> x= 2,  y= 2,    z= 3/4.


You can check it manually (as I did it using Excel in my computer).


Answer.  The given system has 6 solutions listed above.