Question 1090977: Can someone help me?
I need to write the final answer as an ordered triple (x,y,z)
Solve the system for x,y,z
2x+3y-z=4
3x-y+2z=5
x-4y+3z=1
I tried it, but ended up weird.
Thank you.
Found 3 solutions by Alan3354, MathLover1, MathTherapy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve the system for  , , , ,
 .....eq.1 .....eq.1
 .....eq.2 .....eq.2
 .....eq.3 .....eq.3
------------------------------------------
 .....eq.1...solve for .....eq.1...solve for 
 .....eq.(1z) .....eq.(1z)
 .....eq.2..solve for .....eq.2..solve for 

 ....eq.(2z) ....eq.(2z)
 .....eq.3..........solve for .....eq.3..........solve for 

 ....eq.(3z) ....eq.(3z)
from eq.(1z) and eq.(2z):
 ...solve for ...solve for 



 .....(a) .....(a)
from eq.(2z) and eq.(3z):
 ....both sides multiply by ....both sides multiply by 



 .....(b) .....(b)
 .....eq.2....substitute .....eq.2....substitute  and and 
 .....eq.2 .....eq.2
 -> real solution -> real solution
 .....eq.(1z)......substitute .....eq.(1z)......substitute 

 -> real solution -> real solution
 , ,  , ,  , where , where  element element 
integer solutions:
( , , , , )=( )=(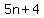 , , 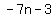 , , 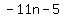 ) )
find some real take real solutions and equal to zero:

 ...solve for ...solve for 



plug in



find  : :


real solutions:( , , , , )=( )=( , , , ,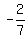 ) )
or
if 
( , , , , )=( )=( , ,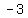 , ,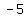 ) )
if 
( , , , , )=( )=( , ,  , ,  ) ...and so on ) ...and so on
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Can someone help me?
I need to write the final answer as an ordered triple (x,y,z)
Solve the system for x,y,z
2x+3y-z=4
3x-y+2z=5
x-4y+3z=1
I tried it, but ended up weird.
Thank you.
2x + 3y - z = 4 -------- eq (i)
3x - y + 2z = 5 -------- eq (ii)
x - 4y + 3z = 1 -------- eq (iii)
I can clearly see what you're saying!
The EASIEST method to be used here is ELIMINATION, as follows:
1) Multiply eq (i) by 2 to get: 4x + 6y - 2z = 8 ---- eq (iv)
2) Add eqs (ii) & (iv) to get: 7x + 5y = 13 --------- eq (v)
1) Multiply eq (i) by 3 to get: 6x + 9y - 3z = 12 --- eq (vi)
2) Add eqs (iii) & (vi) to get: 7x + 5y = 13 -------- eq (vii)
Do you notice anything? If not, it's clear that eqs (v) & (vii) are the same
Therefore, there are an INFINITE number of solutions to this system!
If you want to see what I'm talking about, substitute a value for x in eq (v) or (vii), and then solve for y. You will then have values for x and y.
Substitute these 2 values in any of the 3 ORIGINAL equations (I would choose eq 1 since that equation has a z-value with a coefficient of - 1), and then solve for z.
You now have values for x, y, and z.
Substitute these 3 values into all 3 ORIGINAL equations, and you will see that these values satisfy all 3.
You can follow the same process if you so choose to use a different value for x.
|
|
|