Question 1070691: A new movie theater holds 300 people. They found that when the price was $5 per ticket, the average sales would be 270 people per show. Each time they increase the price by $1, the average attendance drops by 15 people.
A) find an expression, using x, for the number of people that will go to each show
B) find the function R (x) that gives the amount of revenue the theater will make
C) what price should they charge in order to maximize revenue?
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A new movie theater holds 300 people. They found that when the price was $5 per ticket, the average sales would be 270 people
per show. Each time they increase the price by $1, the average attendance drops by 15 people.
A) find an expression, using x, for the number of people that will go to each show
B) find the function R (x) that gives the amount of revenue the theater will make
C) what price should they charge in order to maximize revenue?
~~~~~~~~~~~~~~~~~~~~~
1. Let N(x) be this function: the number of viewers at the ticket price of x dollars.
Then N(x) = 270 - 15(x-5). (1)
It is exact translation of this statement: "Each time they increase the price by $1, the average attendance drops by 15 people."
So, the question A) is answered, and the answer is: the attendance is
N(x) = 270 - 15(x-5) = 345 - 15x.
where x is the ticket price in dollars.
2. The revenue R(x) is R(x) = N(x)*x = x*(345 - 15x) = 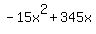 . (2)
See the plot below. So, the question B) is answered, too.
3. The maximum of the quadratic function (2) is achieved at x = . (2)
See the plot below. So, the question B) is answered, too.
3. The maximum of the quadratic function (2) is achieved at x =  = = 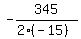 = 11.5.
Thus the optimum price is 11.5 dollars per ticket.
The attendance then is N(11.5) = 270 - 15*(11.5-5) = 172.5 persons. = 11.5.
Thus the optimum price is 11.5 dollars per ticket.
The attendance then is N(11.5) = 270 - 15*(11.5-5) = 172.5 persons.
 Plot y =
Plot y = 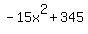
So, at given conditions, the owner of the theater can increase the ticket price to $11.50.
The attendance will decrease to 172 - 173 viewers, but the revenue will increase from 300*$5 = $1500 to 172*$11.50 = $1978.
All questions are answered. The problem is solved.
On finding the maximum/minimum of a quadratic function see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
For similar solved problems on maximazing revenue/profit see the lesson
- Using quadratic functions to solve problems on maximizing revenue/profit
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Finding minimum/maximum of quadratic functions".
|
|
|