SOLUTION: A line intersects the y-axis, the line {{{y = 2x + 2}}}, and the x-axis at the points A, B, and C respectively. If segment AC has a length of {{{4 sqrt(2)}}} units and B lies in th

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: A line intersects the y-axis, the line {{{y = 2x + 2}}}, and the x-axis at the points A, B, and C respectively. If segment AC has a length of {{{4 sqrt(2)}}} units and B lies in th      Log On


   

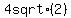Question 1058171: A line intersects the y-axis, the line y+=+2x+%2B+2, and the x-axis at the points A, B, and C respectively. If segment AC has a length of 4+sqrt%282%29 units and B lies in the first quadrant and is the midpoint of segment AC, find the equation of the line in slope-intercept form.
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Let's assume that the line intersects the x-axis at A:(a,0) and the y-axis at C:(0,c).
So you the distance is,
%28a-0%29%5E2%2B%280-c%29%5E2=%284sqrt%282%29%29%5E2
a%5E2%2Bc%5E2=32
You also know that the midpoint is B and using the equation of the midpoint,
x%5Bb%5D=%28a%2B0%29%2F2=a%2F2
and
y%5Bb%5D=%28b%2B0%29%2F2=c%2F2
Since it's a common point between the line and the line y=2x%2B2, then,
c%2F2=2%28a%2F2%29%2B2
c%2F2=a%2B2
c=2a%2B4
Substituting above,
a%5E2%2B%282a%2B4%29%5E2=32
a%5E2%2B4a%5E2%2B16a%2B16=32
5a%5E2%2B16a-16=0
%28a%2B4%29%285a-4%29=0
Since you only allow solutions in Q1, only use the positive solution.
5a-4=0
a=4%2F5
then,
c=2%284%2F5%29%2B20%2F5
c=28%2F5
You can then calculate the slope of the line,
m=%28c-0%29%2F%280-a%29=%2828%2F5%29%2F%28-4%2F5%29=-7
So,
highlight_green%28y=-7x%2B28%2F5%29
.
.
.
.