Question 1042808: I Need help with solving an equation in two variables using elimination method. Here's the sum: 11x - 7y =xy , 9x - 4y = 6xy please.?
Found 3 solutions by stanbon, ikleyn, MathTherapy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 11x - 7y =xy , 9x - 4y = 6xy
----
Solve each for "y"::
y(x+7) = 11x
y = 11x/(x+7)
-----
y(6x+4) = 9x
y = 9x/(6x+4)
----------
Subtract and solve for "x"::
11x/(x+7)-9x/(6x+4) = 0
--------
11x(6x+4) - 9x(x+7) = 0
66x^2 + 24x - 9x^2 - 63x = 0
57x^2 - 39x = 0
x(57x - 39) = 0
x = 0 or x = 39/57 = 13/19
Solve for "y"::
y = 11x/(x+7)
If x = 0, y = 0
If x = 13/19, y = 143/146
---------------
Cheers,
Stan H.
---------------------
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I Need help with solving an equation in two variables using elimination method. Here's the sum: 11x - 7y =xy , 9x - 4y = 6xy please.?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
11x - 7y = xy, (1)
9x - 4y = 6xy. (2)
There is more elegant solution. Let me show it.
Divide both sides of (1) by xy. Divide both sides of (2) by xy. You will get
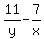 = 1, (1') = 1, (1')
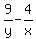 = 6. (2')
Now introduce new variables u = = 6. (2')
Now introduce new variables u =  , v = , v =  . Then (1') and (2') take the form
11u - 7v = 1, (1'')
9u - 4v = 6. (2'')
It is usual system of two linear equations in two unknowns.
You can easily solve it using the Elimination method in its standard form. It is just simple technique, let me do not continue.
When you find u and v, do not forget to return back to the original x and y.
In order to make this approach absolutely clean, you must justify dividing by xy of equations (1) and (2).
It means that you must accurately analyse the case xy = 0.
If xy = 0, then x=0 or y=0 (or both).
If x=0, then from equations (1),(2) y=0.
If y=0, then from equations (1),(2) x=0.
Thus x=0, y=0 is one solution of (1), (2).
The other solution comes from the procedure described above. . Then (1') and (2') take the form
11u - 7v = 1, (1'')
9u - 4v = 6. (2'')
It is usual system of two linear equations in two unknowns.
You can easily solve it using the Elimination method in its standard form. It is just simple technique, let me do not continue.
When you find u and v, do not forget to return back to the original x and y.
In order to make this approach absolutely clean, you must justify dividing by xy of equations (1) and (2).
It means that you must accurately analyse the case xy = 0.
If xy = 0, then x=0 or y=0 (or both).
If x=0, then from equations (1),(2) y=0.
If y=0, then from equations (1),(2) x=0.
Thus x=0, y=0 is one solution of (1), (2).
The other solution comes from the procedure described above.
For close melody problems see the lesson
- Solving systems of non-linear equations in two unknowns using the Cramer's rule
in this site.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|