Question 1039987: x+y+z=12;xy+yz+zx=44;x^3+y^3+z^3=288. Find value of x,y and z.
Found 3 solutions by Boreal, ikleyn, robertb:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! One way to do this is to note that for positive integers, which the answer must contain, the largest must be 6, because any larger would have a negative result for the other two. 6^3 is 216, and that leaves 72. That is the sum of two cubes, 64 (4^3) and 8 (2^3).
6+4+2=12
24+8+12=44.
In number theory a number not in the form of 9k+/-4 can be written as the sum of 3 cubes.
That is as far as I can go.
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
x+y+z=12; xy+yz+zx=44; x^3+y^3+z^3=288. Find value of x,y and z.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 (1) (1)
The previous tutor found the solution by the method of "trial and error".
The question remains still open if it can be solved on the more solid algebraic base.
The answer is "Yes", and I will show you "How".
With one apology: since the problem is slightly higher than the traditional school math, the solution is, correspondingly,
slightly higher (but still understandable).
Part 1. Motivation
We are given the numerical values for the functions 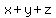 , , 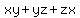 and and 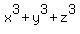 .
A remarkable fact is that the function .
A remarkable fact is that the function 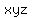 can be explicitly expressed via can be explicitly expressed via 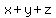 , , 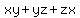 and and 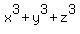 . (I will do it later).
So, knowing the numerical values of . (I will do it later).
So, knowing the numerical values of 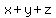 , , 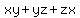 and and 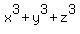 , we can find the value of , we can find the value of 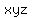 .
Next, knowing the numerical values of .
Next, knowing the numerical values of 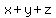 , , 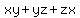 and and 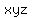 , we can consider the polynomial of the variable "u"
P(u) = , we can consider the polynomial of the variable "u"
P(u) = 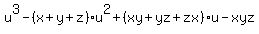 . (2)
This polynomial is nothing else as
P(u) = (u-x)*(u-y)*(u-z). (3)
In other words, the polynomial (2) is factorable into (3).
Now, instead of solving the system (1), we can solve the polynomial equation
P(u) = 0 (4)
for u. If we solve it (and when we solve it), its roots u = x, u = y and u = z will be the solution of the system (1).
Why this way is better than solving (1) directly?
Well, for example, you can (try) to solve the polynomial equation (4) graphically.
Or apply other methods specific for polynomial equations.
You will see it later.
Now I will implement this methodology. . (2)
This polynomial is nothing else as
P(u) = (u-x)*(u-y)*(u-z). (3)
In other words, the polynomial (2) is factorable into (3).
Now, instead of solving the system (1), we can solve the polynomial equation
P(u) = 0 (4)
for u. If we solve it (and when we solve it), its roots u = x, u = y and u = z will be the solution of the system (1).
Why this way is better than solving (1) directly?
Well, for example, you can (try) to solve the polynomial equation (4) graphically.
Or apply other methods specific for polynomial equations.
You will see it later.
Now I will implement this methodology.
Part 2. Calculation of 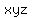 via via 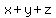 , , 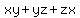 and and 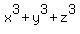
We will do it step by step:
1. 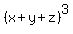 = = 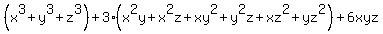 2.
2. 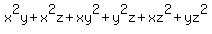 =
= x(xy+xz) + y(xy+yz) + z(xz+yz) =
= x(xy+xz+yz-yz) + y(xy+yz+xz-xz) + z(xz+yz+xy-xy)
= x(xy+xz+yz) + y(xy+xz+yz) + z(xy+xz+yz) - x(yz) - y(xz) - z(xy)
= (x+y+z)(xy+xz+yz) - 3xyz
3. Therefore, =
= x(xy+xz) + y(xy+yz) + z(xz+yz) =
= x(xy+xz+yz-yz) + y(xy+yz+xz-xz) + z(xz+yz+xy-xy)
= x(xy+xz+yz) + y(xy+xz+yz) + z(xy+xz+yz) - x(yz) - y(xz) - z(xy)
= (x+y+z)(xy+xz+yz) - 3xyz
3. Therefore,
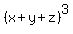 = = 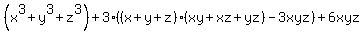 , or , or
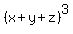 = = 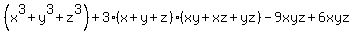 , or , or
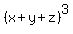 = = 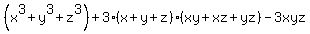 , or
xyz = , or
xyz =  .
4. Thus
xyz = .
4. Thus
xyz =  = = 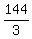 = 48. = 48.
Part 3. Working with the polynomial
So, our polynomial (2) is
P(u) = 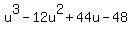 ,
and we need solve this polynomial equation (4) ,
and we need solve this polynomial equation (4)
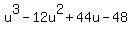 = =  .
First, let's do it graphically. .
First, let's do it graphically.

Figure. Plot P(u) = 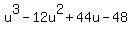
|
Do you see the roots? Of course, they are u=2, u=4 and u=6.
And you can check it manually substituting these values into the polynomial.
Or you can apply the rational roots theorem.
All the roots are among the integer divisors of the number 48, and you have only finite number of options to check.
It is your other method to find the roots.
So, the original problem is solved algebraically.
The solution is x=2, y=3, z=6 and all permutations of these values.
Even more amazing is the fact that all this approach can be extended to the systems of four, five and so on unknowns.
Thanks to the person who submitted this challenging problem.
This solution is my gift to you and to the entire community for the day of July, 4.
Answer by robertb(5830)   (Show Source): (Show Source):
|
|
|