SOLUTION: Solve the following equation for x and y: (2)^2+x +(3)^3+y=275 (2)^3+x +(3)^2+y=145

Since you do not use parentheses properly, there are several ways to read your system.
Your writing is ambiguous. To avoid ambiguity, use parentheses.

Is THIS modification what you want?

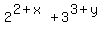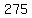 = ,     (1)
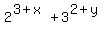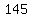 = .     (2)


Below is the solution of this system.


Since 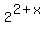 = 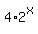,  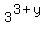= 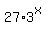,  = 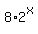,  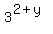= 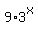, you can rewrite the system (1), (2) in the form

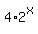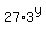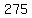 +  = ,      (1')
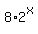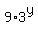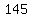 +  = .       (2')

This system is still non-linear.
The way to solve it is to introduce new variables u = 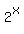 and v = .
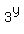Then the system (1'), (2') takes the form

4u + 27v = 275,         (3)
8u +  9v = 145.         (4)

The system (3), (4) is just a linear, and we can easily solve it.
I will use the Elimination method. Multiply equation (3) by 2 (both sides). You will get

8u + 54v = 550,         (3')
8u +  9v = 145.         (4')

Now, distract (3') from (4'). You will get

54v - 9v = 550 - 145  --->  45v = 405  --->  v = 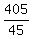 = 9.

Now recall that v = 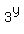,  or  9 = 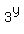.  Hence,  y = 2,  and one unknown is just found.

Next, from (3)  u = 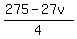 =  =  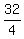= 8.

Again, recall that  u = 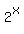,  or 8 = 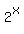.  Hence,  x = 3.

The problem is solved.

Answer.  x = 3,  y = 2.

You can check that the solution is correct.