SOLUTION: pLEASE HELP ME I AM SO CONFUSED BEEN OUT OF SCHOOL FOR OVER 30YRS AND NEVER HAD PROBLEMS LIKE THIS 1.Maricopa's Success scholarship fund receives a gift of $ 120000. The money i

Algebra ->  Coordinate Systems and Linear Equations  -> Lessons -> SOLUTION: pLEASE HELP ME I AM SO CONFUSED BEEN OUT OF SCHOOL FOR OVER 30YRS AND NEVER HAD PROBLEMS LIKE THIS 1.Maricopa's Success scholarship fund receives a gift of $ 120000. The money i      Log On


   

Question 1025670: pLEASE HELP ME I AM SO CONFUSED BEEN OUT OF SCHOOL FOR OVER 30YRS AND NEVER HAD PROBLEMS LIKE THIS
1.Maricopa's Success scholarship fund receives a gift of $ 120000. The money is invested in stocks, bonds, and CDs. CDs pay 4 % interest, bonds pay 2 % interest, and stocks pay 7.7 % interest. Maricopa Success invests $ 35000 more in bonds than in CDs. If the annual income from the investments is $ 5835 , how much was invested in each account?
Maricopa Success invested $ in stocks.
Maricopa Success invested $ in bonds.
Maricopa Success invested $ in CDs.

2.A chemist has three different acid solutions. The first acid solution contains 25% acid, the second contains 35% and the third contains 55%. He wants to use all three solutions to obtain a mixture of 75 liters containing 45%acid, using 3 times as much of the 55% solution as the 35% solution. How many liters of each solution should be used?
The chemist should use
liters of 25% solution,
liters of 35% solution, and
liters of 55% solution.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
The two questions are almost the same kind. I will do just your #2 mixture percents question.

x,y,z for the low, medium, and high(er) concentration acids. The quantities of them IN LITERS to use.

...using 3 times as much of the 55% solution as the 35% solution.
This means z%2Fy=3, and from this, z=3y.

Make the material sum equation.
x%2By%2Bz=75, which you may use later.

Substituting for z, the material sum is also x%2By%2B3y=75,
x%2B4y=75.

Make the percentage relationship equation for the mixture to prepare.
%2825x%2B35y%2B55z%29%2F%2875%29=45, which you might need effort to understand.
-
Again substitute for z in this percents equation.
%2825x%2B35y%2B55%2A3y%29%2F75=45

%2825x%2B200y%29%2F75=45
and you should reduce this, since it can be reduced.

%285%28x%2B40y%29%29%2F75=5%2A9

%28x%2B40y%29%2F75=9

-
Summarize your equations as a system, keeping in mind, you temporarily eliminated z.
-
highlight_green%28system%28x%2B4y=75%2C%28x%2B40y%29%2F75=9%29%29
This is your system to solve for x and y. This IS a linear system; just multiply the members of the percents equation by 75.

highlight_green%28system%28x%2B4y=75%2Cx%2B40y=675%29%29

If you not remember how to use Elimination Method, then just use Substitution Method.
-
x=75-4y
-
%2875-4y%29%2B40y=675
75-4y%2B40y=675
36y=600
y=600%2F36
y=300%2F18
y=150%2F9
highlight%28y=50%2F3%29
or
highlight%28y=16%262%2F3%29----------the 35% acid, liters to use
-
FIND x.
x=75-4%2A%2816%262%2F3%29
highlight%28x=8%261%2F3%29---------liters to use of the 25% acid

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
pLEASE HELP ME I AM SO CONFUSED BEEN OUT OF SCHOOL FOR OVER 30YRS AND NEVER HAD PROBLEMS LIKE THIS
1.Maricopa's Success scholarship fund receives a gift of $ 120000. The money is invested in stocks, bonds, and CDs. CDs pay 4 % interest, bonds pay 2 % interest, and stocks pay 7.7 % interest. Maricopa Success invests $ 35000 more in bonds than in CDs. If the annual income from the investments is $ 5835 , how much was invested in each account?
Maricopa Success invested $ in stocks.
Maricopa Success invested $ in bonds.
Maricopa Success invested $ in CDs.

2.A chemist has three different acid solutions. The first acid solution contains 25% acid, the second contains 35% and the third contains 55%. He wants to use all three solutions to obtain a mixture of 75 liters containing 45%acid, using 3 times as much of the 55% solution as the 35% solution. How many liters of each solution should be used?
The chemist should use
liters of 25% solution,
liters of 35% solution, and
liters of 55% solution.
Let amount invested in CDs be C

Then amount invested in bonds = C + 35,000

Thus, amount invested in stocks = 120,000 - (C + C + 35,000), or 120,000 - (2C + 35,000), or 120,000 - 2C - 35,000, or 85,000 - 2C

We then get: .04(C) + .02(C + 35,000) + .077(85,000 - 2C) = 5,835

.04C + .02C + 700 + 6,545 - .154C = 5,835

.04C + .02C - .154C = 5,835 - 7,245

- .094C = - 1,410 

C, or amount invested in CDs = 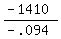%28-+1410%29%2F%28-+.094%29, or highlight_green%28matrix%281%2C1%2C%22%2415%2C000%22%29%29

Amount invested in bonds: $15,000 + 35,000, or highlight_green%28matrix%281%2C1%2C%22%2450%2C000%22%29%29

Amount invested in stocks: $120,000 - (15,000 + 50,000) = $120,000 - 65,000, or highlight_green%28matrix%281%2C1%2C%22%2455%2C000%22%29%29

=====================

2.

Let amount of 35% acid to be mixed, be T

Then amount of 55% acid to be mixed = 3T

Amount of 25% acid to be mixed = 75 - (T + 3T), or 75 - 4T

We then get: .35(T) + .55(3T) + .25(75 - 4T) = .45(75)

.35T + 1.65T + 18.75 - T = 33.75

.35T + 1.65T - T = 33.75 - 18.75

T, or amount of 35% acid to be mixed = highlight_green%28matrix%281%2C2%2C+15%2C+L%29%29

Amount of 55% acid to be mixed: 3(15), or highlight_green%28matrix%281%2C2%2C+45%2C+L%29%29

Amount of 25% acid to be mixed: 75 - (15 + 45) = 75 - 60, or highlight_green%28matrix%281%2C2%2C+15%2C+L%29%29