Question 1011120: Solve the four equations simultaneously ,
2a+c=0
3a+2b+d=3
a+3b+c=2
b+d= -1
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! More ways than just one. I would try eliminating or substituting for a, using the third-row equation, as  . Simplify the resulting system and you will have THREE equations in THREE unknown variables. . Simplify the resulting system and you will have THREE equations in THREE unknown variables.
What you do may depend on what skills you are being taught. Matrices? Simple linear systems in Elementary/Intro Algebra 1 ?
---
Part of but not the whole solution,

Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the four equations simultaneously
2a + c = 0 (1)
3a + 2b + d = 3 (2)
a + 3b + c = 2 (3)
b + d = -1 (4)
---------------------------------------
Express c = -2a from (1) and substitute it into (3). You will get
a + 3b - 2a = 3, or
-a + 3b = 2 (3')
Next, express d = -1 - b from(4) and substitute it into (2). You will get
3a + 2b + (-1 - b) = 3, or
3a + b = 4 (2').
Now you have this system of two equation in two unknowns (3') and (2').
To solve it, express b = 4 - 3a from (2') and substitute it into (3'). You will get
-a + 3*(4 - 3a) = 2 -----> -a - 9a = 2 - 12 -----> -10a = - 10 -----> a = 1.
Then from (2') b = 4 - 3a = 4 - 3 = 1.
Finally, from (1) c = -2a = -2*1 = -2;
from (4) d = -1 - b = -1 - 1 = -2.
Answer. a = 1; b = 1; c = -2; d = -2.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Solve the four equations simultaneously ,
2a+c=0
3a+2b+d=3
a+3b+c=2
b+d= -1
2a + c = 0 ----- eq (i)
3a + 2b + d = 3 ----- eq (ii)
a + 3b + c = 2 ----- eq (iii)
b + d = - 1 ----- eq (iv)
a - 3b = - 2 ------ Subtracting eq (iii) from eq (i) -------- eq (v)
3a + b = 4 ------ Subtracting eq (iv) from eq (ii) -------- eq (vi)
– 3a + 9b = 6 ------ Multiplying eq (v) by – 3 ------- eq (vii)
10b = 10 ------ Adding eqs (vii) & (vi)
b = 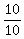 , or 1 , or 1
a - 3(1) = - 2 ----- Substituting 1 for b in eq (v)
a – 3 = - 2
a = - 2 + 3, or 1
1 + d = - 1 -------- Substituting 1 for b in eq (iv)
d = - 1 – 1, or - 2
2(1) + c = 0 ------- Substituting 1 for a in eq (i)
2 + c = 0
c = - 2

|
|
|