Tutors Answer Your Questions about Linear-systems (FREE)
Question 1209934: a firm hires 7 technicians and 3 apprentices for total daily wages of 820. if one apprentice is appointed to a technician, the total daily wages become 880. What are thr daily wages for a technician and an apprentice
Found 5 solutions by greenestamps, josgarithmetic, ikleyn, angelatoyogon, CPhill:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a quick and easy informal mental solution to the problem.
The combined wages of 7 technicians and 3 apprentices is 820.
When one apprentice becomes a technician, the combined wages of 8 technicians and 2 apprentices is 880.
So when an apprentice becomes a technician, the combined wages go up by 60.
Have that happen twice more, ending up with 10 technicians and 0 apprentices. The combined wages is now 880 + 60 + 60 = 1000.
So the wage for each technician is 1000/10 = 100.
When there were 7 technicians and 3 apprentices, the total wages was 820. The wages for the 7 technicians was 7*100 = 700, so the wages for the 3 apprentices was 820-700 = 120; so the wage for each apprentice is 120/3 = 40.
Alternatively, once we find that the wages for each technician is 100, we can use the fact that the total wages increase by 60 each time an apprentice becomes a technician to determine that the wage for each apprentice is 100-60 = 40.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! Apprentice day pay rate, x
Technician day pay rate, y
Initially 3 apprentices and 7 technicians
PAY-RATE TIME(day count) WAGE
APPRENTICES x 1 3x
TECHNICIANS y 1 7y
Total 820
one less apprentice and one more technicin
PAY-RATE TIME(day count) WAGE (total)
APPRENTICES x 1 2x
TECHNICIANS y 1 8y
Total 880
 ------Solve this system. ------Solve this system.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a firm hires 7 technicians and 3 apprentices for total daily wages of 820.
if one apprentice is appointed to a technician, the total daily wages become 880.
What are the daily wages for a technician and an apprentice
~~~~~~~~~~~~~~~~~~~~~~
Dear Angela,
as I see, you are first time at this forum.
You are welcome, we are glad to every newcomer !
You came with the problem, which was posted to the forum earlier (two or three months ago),
and for which the solution was just developed and placed at this forum by the other tutor
exactly at the same spot, from which you submitted your post.
So, I will assume that you just have read that solution. It is correct, so I do not see
any need to re-tell or to re-write it again.
At these circumstances, it is not precisely clear to me the meaning of your request.
For us, it would be much easier to communicate, if you formulate the goal of your visit
with the problem, which was just solved before.
I may to suspect that the problem's formulation is not fully clear to you.
To be honest, as written in the post, it is not clear to me, too.
In my view, the problem formulation in the post is not as clear as it should be in Math problems,
and requires to be explained.
Had I formulate this problem, I would make it differently. I would write
A firm hires 7 technicians and 3 apprentices for total daily wages of 820.
Later, one of the 3 apprentices was appointed to a position of technician,
and, therefore, the total daily wages became 880.
What are the daily wages for a technician and an apprentice ?
Now everything is clear, everything is transparent, the meaning is clear and additional clarifications are not needed.
It is how Math problem should be formulated, when it goes outside.
I grew and got my mathematical education in other country, where a clear formulation
of school Math problems was mandatory, and an unclear formulation had no chance to see a world.
Here in US it is not so. At every corner, you can find formulations of Math problems,
that do not stand up to any criticism.
Also, in the Internet era, thousands of people that have no adequate Math education,
think that they can create and disseminate their own math problems in the Internet.
But it is the reality in which we live.
In any case, I am glad you visited this website/forum, and hope that you will find here
many useful conversations/communications/information/solutions/ideas/advises for your Math education.
Answer by angelatoyogon(1)  (Show Source): (Show Source):
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's use variables to represent the daily wages:
* Let 't' represent the daily wage of a technician.
* Let 'a' represent the daily wage of an apprentice.
We can set up two equations based on the given information:
**Equation 1:** 7 technicians and 3 apprentices earn 820.
* 7t + 3a = 820
**Equation 2:** If one apprentice becomes a technician, there are 8 technicians and 2 apprentices, and they earn 880.
* 8t + 2a = 880
Now we have a system of two linear equations with two variables. We can solve for 't' and 'a'.
**Solve the System of Equations:**
We can use the substitution or elimination method. Let's use the elimination method.
1. Multiply Equation 1 by 2 and Equation 2 by 3 to make the 'a' coefficients match:
* (7t + 3a = 820) * 2 => 14t + 6a = 1640
* (8t + 2a = 880) * 3 => 24t + 6a = 2640
2. Subtract the first modified equation from the second modified equation to eliminate 'a':
* (24t + 6a) - (14t + 6a) = 2640 - 1640
* 10t = 1000
3. Solve for 't':
* t = 1000 / 10
* t = 100
4. Substitute the value of 't' back into either Equation 1 or Equation 2 to solve for 'a'. Let's use Equation 1:
* 7(100) + 3a = 820
* 700 + 3a = 820
* 3a = 820 - 700
* 3a = 120
5. Solve for 'a':
* a = 120 / 3
* a = 40
**Answers:**
* The daily wage of a technician (t) is $100.
* The daily wage of an apprentice (a) is $40.
Question 1169746: 4) The equations defining a model of two trading nations are given by
𝑌 𝑌 𝐶1 = 0.7𝑌1 + 50 𝐶2 = 0.8𝑌2 + 100 𝐼 𝐼 𝑀1 = 0.3𝑌1 𝑀2 = 0.1𝑌2
a. Express this system in matrix form and hence find the values of 𝑌1 and 𝑌2.
b.Calculate the balance of payments between these countries
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step.
**Understanding the Model**
We are given a model of two trading nations, with the following equations:
* **Country 1:**
* Y1 = C1 + I1 + X1 - M1
* C1 = 0.7Y1 + 50
* M1 = 0.3Y1
* **Country 2:**
* Y2 = C2 + I2 + X2 - M2
* C2 = 0.8Y2 + 100
* M2 = 0.1Y2
Where:
* Y = National Income
* C = Consumption
* I = Investment (we'll assume I1 and I2 are exogenous, so we'll treat them as constants)
* X = Exports
* M = Imports
We also know that:
* X1 = M2 (Exports of country 1 are imports of country 2)
* X2 = M1 (Exports of country 2 are imports of country 1)
**a) Express the System in Matrix Form and Find Y1 and Y2**
1. **Substitute the Equations:**
* For Country 1:
* Y1 = (0.7Y1 + 50) + I1 + M2 - 0.3Y1
* Y1 = 0.4Y1 + 50 + I1 + 0.1Y2
* 0.6Y1 - 0.1Y2 = 50 + I1
* For Country 2:
* Y2 = (0.8Y2 + 100) + I2 + M1 - 0.1Y2
* Y2 = 0.7Y2 + 100 + I2 + 0.3Y1
* -0.3Y1 + 0.3Y2 = 100 + I2
2. **Matrix Form:**
We can write this system of equations in matrix form as:
```
[ 0.6 -0.1 ] [ Y1 ] = [ 50 + I1 ]
[ -0.3 0.3 ] [ Y2 ] = [ 100 + I2 ]
```
Let's represent this as:
```
A * Y = B
```
Where:
```
A = [ 0.6 -0.1 ]
[ -0.3 0.3 ]
Y = [ Y1 ]
[ Y2 ]
B = [ 50 + I1 ]
[ 100 + I2 ]
```
3. **Solve for Y (Y1 and Y2):**
To find Y, we need to calculate A⁻¹ and multiply it by B:
```
Y = A⁻¹ * B
```
First, find the determinant of A:
* det(A) = (0.6 * 0.3) - (-0.1 * -0.3) = 0.18 - 0.03 = 0.15
Now, find the inverse of A:
```
A⁻¹ = (1 / det(A)) * [ 0.3 0.1 ]
[ 0.3 0.6 ]
A⁻¹ = (1 / 0.15) * [ 0.3 0.1 ]
[ 0.3 0.6 ]
A⁻¹ = [ 2 2/3 ]
[ 2 4 ]
```
Now, multiply A⁻¹ by B:
```
Y = [ 2 2/3 ] [ 50 + I1 ]
[ 2 4 ] [ 100 + I2 ]
Y1 = 2(50 + I1) + (2/3)(100 + I2)
Y1 = 100 + 2I1 + 200/3 + (2/3)I2
Y1 = 500/3 + 2I1 + (2/3)I2
Y2 = 2(50 + I1) + 4(100 + I2)
Y2 = 100 + 2I1 + 400 + 4I2
Y2 = 500 + 2I1 + 4I2
```
**b) Calculate the Balance of Payments Between These Countries**
The balance of payments is the difference between exports and imports.
* Balance of Payments for Country 1 = X1 - M1 = M2 - M1 = 0.1Y2 - 0.3Y1
* Balance of Payments for Country 2 = X2 - M2 = M1 - M2 = 0.3Y1 - 0.1Y2
Let's calculate the balance of payments for Country 1:
* Balance of Payments 1 = 0.1Y2 - 0.3Y1
* Balance of Payments 1 = 0.1(500 + 2I1 + 4I2) - 0.3(500/3 + 2I1 + (2/3)I2)
* Balance of Payments 1 = 50 + 0.2I1 + 0.4I2 - 50 - 0.6I1 - 0.2I2
* Balance of Payments 1 = -0.4I1 + 0.2I2
Let's calculate the balance of payments for Country 2:
* Balance of Payments 2 = 0.3Y1 - 0.1Y2
* Balance of Payments 2 = 0.3(500/3 + 2I1 + (2/3)I2) - 0.1(500 + 2I1 + 4I2)
* Balance of Payments 2 = 50 + 0.6I1 + 0.2I2 - 50 - 0.2I1 - 0.4I2
* Balance of Payments 2 = 0.4I1 - 0.2I2
**Conclusion**
* Y1 = 500/3 + 2I1 + (2/3)I2
* Y2 = 500 + 2I1 + 4I2
* Balance of Payments for Country 1 = -0.4I1 + 0.2I2
* Balance of Payments for Country 2 = 0.4I1 - 0.2I2
The balance of payments for Country 2 is the negative of the balance of payments for Country 1, meaning that if one country has a surplus, the other has a deficit.
Question 1173100: Mr.Agoncillo has a savings account in two banks. The combined amount of these savings is at least Php 150,000. One bank gives an interest of 4% while the other bank give 6%. In a year, Mr. Agoncillo receive at most Php. 12,000.
Write and graph a system of linear inequalities that shows all the posible solutions.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem and set up the system of linear inequalities.
**Variables**
* Let 'x' represent the amount of savings in the bank with 4% interest.
* Let 'y' represent the amount of savings in the bank with 6% interest.
**Inequalities**
1. **Combined Savings:**
* The combined amount of savings is at least Php 150,000.
* Equation: x + y ≥ 150,000
2. **Interest Earned:**
* The total interest earned is at most Php 12,000.
* Interest from 4% bank: 0.04x
* Interest from 6% bank: 0.06y
* Equation: 0.04x + 0.06y ≤ 12,000
3. **Non-negative Savings:**
* Savings cannot be negative.
* Equations: x ≥ 0 and y ≥ 0
**System of Linear Inequalities**
* x + y ≥ 150,000
* 0.04x + 0.06y ≤ 12,000
* x ≥ 0
* y ≥ 0
**Graphing the Inequalities**
1. **x + y ≥ 150,000**
* To graph this, first graph the line x + y = 150,000.
* Find the intercepts:
* If x = 0, y = 150,000
* If y = 0, x = 150,000
* Draw the line connecting (150000,0) and (0,150000). Since the inequality is "greater than or equal to," use a solid line.
* Shade the region above the line, as that represents x + y ≥ 150,000.
2. **0.04x + 0.06y ≤ 12,000**
* To graph this, first graph the line 0.04x + 0.06y = 12,000.
* To make it easier to graph, we can multiply the entire equation by 100
* 4x+6y=1200000
* Then we can divide the entire equation by 2
* 2x+3y=600000
* Find the intercepts:
* If x = 0, 3y = 600000, y = 200,000
* If y = 0, 2x = 600000, x = 300,000
* Draw the line connecting (300000, 0) and (0, 200000). Since the inequality is "less than or equal to," use a solid line.
* Shade the region below the line, as that represents 0.04x + 0.06y ≤ 12,000.
3. **x ≥ 0 and y ≥ 0**
* These inequalities restrict the solution to the first quadrant (where both x and y are non-negative).
**Finding the Solution Region**
* The solution region is the area where all shaded regions overlap in the first quadrant.
* The corner points of this region are important for finding specific solutions.
**Corner Points**
* Intersection of x + y = 150,000 and x = 0: (0, 150,000)
* Intersection of x + y = 150,000 and 0.04x + 0.06y = 12,000:
* Solve the system of equations.
* From x + y = 150,000, y = 150,000 - x.
* Substitute into 0.04x + 0.06(150,000 - x) = 12,000
* 0.04x + 9,000 - 0.06x = 12,000
* -0.02x = 3,000
* x = -150000. There is an error.
* multiply 0.04x + 0.06y = 12000 by 100. 4x+6y=1200000, then divide by 2. 2x+3y=600000
* multiply x+y=150000 by 2. 2x+2y=300000. Substract that from 2x+3y=600000. y=300000. x=-150000. There is still an error.
* Multiply x+y=150000 by 0.04. 0.04x+0.04y=6000.
* Subtract that from 0.04x+0.06y=12000. 0.02y=6000. y=300000. x=150000-300000. x=-150000. There is still an error.
* 0.04x + 0.06(150000-x)=12000
* 0.04x +9000-0.06x=12000
* -0.02x=3000
* x=-150000
* There is an error with the problem itself. The intersection of those two lines is outside of the first quadrant.
* Intersection of 0.04x + 0.06y = 12,000 and y = 0: (300,000, 0)
* Intersection of x=0 and y=0 (0,0)
The solution region is the area between the lines, and within the first quadrant.
Question 1174275: A certain mobile company offers a monthly plan of Php 799 and an additional charge of Php 7.50 per minute when calling to other networks.How much is the monthly bill if the costumer made a 5 minute call to other networks?
A.What is the independent and dependent variable?
B.What is the slope,y-intercept and the linear inequalities?''.
C.What is the value of y?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem.
A. Independent and Dependent Variables
Independent Variable: The number of minutes spent calling other networks (let's call it 'x').
Dependent Variable: The total monthly bill (let's call it 'y').
B. Slope, Y-intercept, and Linear Equation
Fixed Monthly Fee: Php 799
Cost per Minute: Php 7.50
Linear Equation (Slope-Intercept Form):
y = mx + b
Where:
m = slope (cost per minute)
b = y-intercept (fixed monthly fee)
Therefore, the equation is: y = 7.50x + 799
Slope: 7.50 (This represents the cost per minute of calling other networks)
Y-intercept: 799 (This represents the fixed monthly fee)
C. Value of Y (Total Monthly Bill)
The customer made a 5-minute call to other networks (x = 5).
Substitute x = 5 into the equation:
y = 7.50(5) + 799
y = 37.50 + 799
y = 836.50
Answer: The total monthly bill is Php 836.50.
Question 1176798: Determine which of A-D form a solution to the given system for any choice of the free parameter s1. List all letters that apply. If there is more than one answer, type them as a comma separated list.
-8x1 + 3x2 + 15x3 = -52
-3x1 + x2 + 6x3 = -20
HINT: All of the parameters of a solution must cancel completely when substituted into each equation.
a)(5+3s1,7-6s1,s1)
b)(8+3s1,4+3s1,s1)
c)(4+s1,s1,-(4-s1/3))
d)(-(6-3s1/16),s1,-(2-2s1/45))
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's test each solution by substituting the given expressions for x1, x2, and x3 into the equations:
**a) (5 + 3s1, 7 - 6s1, s1)**
* Equation 1: -8(5 + 3s1) + 3(7 - 6s1) + 15s1 = -40 - 24s1 + 21 - 18s1 + 15s1 = -19 - 27s1
* Equation 2: -3(5 + 3s1) + (7 - 6s1) + 6s1 = -15 - 9s1 + 7 - 6s1 + 6s1 = -8 - 9s1
Neither equation is satisfied for all s1.
**b) (8 + 3s1, 4 + 3s1, s1)**
* Equation 1: -8(8 + 3s1) + 3(4 + 3s1) + 15s1 = -64 - 24s1 + 12 + 9s1 + 15s1 = -52
* Equation 2: -3(8 + 3s1) + (4 + 3s1) + 6s1 = -24 - 9s1 + 4 + 3s1 + 6s1 = -20
Both equations are satisfied for all s1.
**c) (4 + s1, s1, -(4 - s1/3))**
* Equation 1: -8(4 + s1) + 3s1 + 15(-(4 - s1/3)) = -32 - 8s1 + 3s1 - 60 + 5s1 = -92
* Equation 2: -3(4 + s1) + s1 + 6(-(4 - s1/3)) = -12 - 3s1 + s1 - 24 + 2s1 = -36
Neither equation is satisfied for all s1.
**d) (-(6 - 3s1/16), s1, -(2 - 2s1/45))**
* Equation 1: -8(-(6 - 3s1/16)) + 3s1 + 15(-(2 - 2s1/45)) = 48 - 3s1/2 + 3s1 - 30 + 2s1/3 = 18 + 5s1/6
* Equation 2: -3(-(6 - 3s1/16)) + s1 + 6(-(2 - 2s1/45)) = 18 - 9s1/16 + s1 - 12 + 4s1/15 = 6 + 191s1/240
Neither equation is satisfied for all s1.
**Conclusion**
Only solution **b) (8 + 3s1, 4 + 3s1, s1)** satisfies the system of equations for all values of s1.
**Answer:** b
Question 1209773: If a_1, a_2, ..., a_19 satisfy
a_1 + a_2 + a_3 + a_4 = 1,
a_2 + a_3 + a_4 + a_5 = 2,
a_3 + a_4 + a_5 + a_6 = 3,
...
a_{16} + a_{17} + a_{18} + a_{19} = 16,
a_{17} + a_{18} + a_{19} + a_1 = 17,
a_{18} + a_{19} + a_1 + a_2 = 18,
a_{19} + a_1 + a_2 + a_3 = 19,
what is the value of a_19?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If a_1, a_2, ..., a_19 satisfy
a_1 + a_2 + a_3 + a_4 = 1,
a_2 + a_3 + a_4 + a_5 = 2,
a_3 + a_4 + a_5 + a_6 = 3,
...
a_{16} + a_{17} + a_{18} + a_{19} = 16,
a_{17} + a_{18} + a_{19} + a_1 = 17,
a_{18} + a_{19} + a_1 + a_2 = 18,
a_{19} + a_1 + a_2 + a_3 = 19,
what is the value of a_19?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution and the final answer in the post by @CPhill are INCORRECT.
The idea is good and the implementation is good until some point.
After this point, implementation is wrong.
So, I will copy-paste the solution by @CPhill below in my post.
Then I will mark there the point till which the solution is correct.
After this point, I will place my calculations, and will complete the solution to the end.
Let's analyze the given system of equations.
We have:
1. a_1 + a_2 + a_3 + a_4 = 1
2. a_2 + a_3 + a_4 + a_5 = 2
3. a_3 + a_4 + a_5 + a_6 = 3
...
16. a_16 + a_17 + a_18 + a_19 = 16
17. a_17 + a_18 + a_19 + a_1 = 17
18. a_18 + a_19 + a_1 + a_2 = 18
19. a_19 + a_1 + a_2 + a_3 = 19
Subtract equation (1) from equation (2):
(a_2 + a_3 + a_4 + a_5) - (a_1 + a_2 + a_3 + a_4) = 2 - 1
a_5 - a_1 = 1
a_5 = a_1 + 1
Subtract equation (2) from equation (3):
(a_3 + a_4 + a_5 + a_6) - (a_2 + a_3 + a_4 + a_5) = 3 - 2
a_6 - a_2 = 1
a_6 = a_2 + 1
In general, we have a_{n+4} = a_n + 1.
This means:
a_5 = a_1 + 1
a_9 = a_5 + 1 = a_1 + 2
a_13 = a_9 + 1 = a_1 + 3
a_17 = a_13 + 1 = a_1 + 4
Similarly,
a_6 = a_2 + 1
a_10 = a_6 + 1 = a_2 + 2
a_14 = a_10 + 1 = a_2 + 3
a_18 = a_14 + 1 = a_2 + 4
Also,
a_7 = a_3 + 1
a_11 = a_7 + 1 = a_3 + 2
a_15 = a_11 + 1 = a_3 + 3
a_19 = a_15 + 1 = a_3 + 4
And,
a_8 = a_4 + 1
a_12 = a_8 + 1 = a_4 + 2
a_16 = a_12 + 1 = a_4 + 3
Now let's use equations 1, 17, 18, and 19.
From eq. 1 --> a_1 + a_2 + a_3 + a_4 = 1
From eq.17 --> a_17 + a_18 + a_19 + a_1 = 17
From eq.18 --> a_18 + a_19 + a_1 + a_2 = 18
From eq.19 --> a_19 + a_1 + a_2 + a_3 = 19 (*)
Substituting the expressions we found:
17. (a_1 + 4) + (a_2 + 4) + (a_3 + 4) + a_1 = 17
2a_1 + a_2 + a_3 + 12 = 17
2a_1 + a_2 + a_3 = 5 (17)
18. (a_2 + 4) + (a_3 + 4) + a_1 + a_2 = 18
a_1 + 2a_2 + a_3 + 8 = 18
a_1 + 2a_2 + a_3 = 10 (18)
19. (a_3 + 4) + a_1 + a_2 + a_3 = 19
a_1 + a_2 + 2a_3 + 4 = 19
a_1 + a_2 + 2a_3 = 15 (19)
<<<---=== till this point, the solution by @CPhill is correct.
After this point, it is WRONG.
<<<---=== So, starting from this point, my solution is going.
20. Add equations (17), (18) and (19). You will get
4a_1 + 4a_2 + 4a_3 = 5 + 10 + 15
4a_1 + 4a_2 + 4a_3 = 30.
Divide both sides by 4
a_1 + a_2 + a_3 = 7.5. (20)
Now we are on the finish line.
From equation (17) subtract equation (20). You will get a_1 = 5 - 7.5 = -2.5.
From equation (18) subtract equation (20). You will get a_2 = 10 - 7.5 = 2.5.
From equation (19) subtract equation (20). You will get a_3 = 15 - 7.5 = 7.5.
From equation (*), a_19 = 19 - a_1 - a_2 - a_3 = 19 - 0 - (-2.5) - 2.5 - 7.5 = 11.5
For completeness, let's determine a_1 from the very first equation in this post
a_1 = 1 - (a_2 + a_3 + a_4) = 1 - ((-2.5) + 2.5 + 7.5) = 1 - 7.5 = -6.5.
From this point, all 19 terms a_1, a_2, a_3, a_4, a_5, . . . , a_19 can be determined.
See this table below
a_1 a_2 a_3 a_4 a_5 a_6 a_7 a_8 a_9 a_10 a_11 a_12 a_13 a_14 a_15 a_16 a_17 a_18 a_19
-2.5 2.5 7.5 -6.5 -1.5 3.5 8.5 -5.5 -0.5 4.5 9.5 -4.5 0.5 5.5 10.5 5.5 1.5 6.5 11.5
You may check that all given 19 original equations are satisfied.
Final Answer: The final answer is a_19 = 11.5.
Solved completely and correctly.
//////////////////////////////////
By the way, I looked at the solution by Google AI for this problem of today, 03/02/25. The link to it is
https://www.google.com/search?q=If+a_1%2C+a_2%2C+...%2C+a_19+satisfy+a_1+%2B+a_2+%2B+a_3+%2B+a_4+%3D+1%2C+a_2+%2B+a_3+%2B+a_4+%2B+a_5+%3D+2%2C+a_3+%2B+a_4+%2B+a_5+%2B+a_6+%3D+3%2C+...+a_%7B16%7D+%2B+a_%7B17%7D+%2B+a_%7B18%7D+%2B+a_%7B19%7D+%3D+16%2C+a_%7B17%7D+%2B+a_%7B18%7D+%2B+a_%7B19%7D+%2B+a_1+%3D+17%2C+a_%7B18%7D+%2B+a_%7B19%7D+%2B+a_1+%2B+a_2+%3D+18%2C+a_%7B19%7D+%2B+a_1+%2B+a_2+%2B+a_3+%3D+19%2C+what+is+the+value+of+a_19%3F&rlz=1C1CHBF_enUS1071US1071&oq=If+a_1%2C+a_2%2C+...%2C+a_19+satisfy+++a_1+%2B+a_2+%2B+a_3+%2B+a_4+%3D+1%2C++a_2+%2B+a_3+%2B+a_4+%2B+a_5+%3D+2%2C++a_3+%2B+a_4+%2B+a_5+%2B+a_6+%3D+3%2C+++...++a_%7B16%7D+%2B+a_%7B17%7D+%2B+a_%7B18%7D+%2B+a_%7B19%7D+%3D+16%2C+a_%7B17%7D+%2B+a_%7B18%7D+%2B+a_%7B19%7D+%2B+a_1+%3D+17%2C++a_%7B18%7D+%2B+a_%7B19%7D+%2B+a_1+%2B+a_2+%3D+18%2C++a_%7B19%7D+%2B+a_1+%2B+a_2+%2B+a_3+%3D+19%2C+++what+is+the+value+of+a_19%3F&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCTE5NjZqMGoxNagCCLACAfEFoMFf_ttl--Y&sourceid=chrome&ie=UTF-8
This solution was slightly different from that by @CPhill, but also was WRONG.
Naturally, I reported them about their wrong solution.
Hope they will fix their artificial mind.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze the given system of equations.
We have:
1. a_1 + a_2 + a_3 + a_4 = 1
2. a_2 + a_3 + a_4 + a_5 = 2
3. a_3 + a_4 + a_5 + a_6 = 3
...
16. a_16 + a_17 + a_18 + a_19 = 16
17. a_17 + a_18 + a_19 + a_1 = 17
18. a_18 + a_19 + a_1 + a_2 = 18
19. a_19 + a_1 + a_2 + a_3 = 19
Subtract equation (1) from equation (2):
(a_2 + a_3 + a_4 + a_5) - (a_1 + a_2 + a_3 + a_4) = 2 - 1
a_5 - a_1 = 1
a_5 = a_1 + 1
Subtract equation (2) from equation (3):
(a_3 + a_4 + a_5 + a_6) - (a_2 + a_3 + a_4 + a_5) = 3 - 2
a_6 - a_2 = 1
a_6 = a_2 + 1
In general, we have a_{n+4} = a_n + 1.
This means:
a_5 = a_1 + 1
a_9 = a_5 + 1 = a_1 + 2
a_13 = a_9 + 1 = a_1 + 3
a_17 = a_13 + 1 = a_1 + 4
Similarly,
a_6 = a_2 + 1
a_10 = a_6 + 1 = a_2 + 2
a_14 = a_10 + 1 = a_2 + 3
a_18 = a_14 + 1 = a_2 + 4
Also,
a_7 = a_3 + 1
a_11 = a_7 + 1 = a_3 + 2
a_15 = a_11 + 1 = a_3 + 3
a_19 = a_15 + 1 = a_3 + 4
And,
a_8 = a_4 + 1
a_12 = a_8 + 1 = a_4 + 2
a_16 = a_12 + 1 = a_4 + 3
Now let's use equations 1, 17, 18, and 19.
1. a_1 + a_2 + a_3 + a_4 = 1
17. a_17 + a_18 + a_19 + a_1 = 17
18. a_18 + a_19 + a_1 + a_2 = 18
19. a_19 + a_1 + a_2 + a_3 = 19
Substituting the expressions we found:
17. (a_1 + 4) + (a_2 + 4) + (a_3 + 4) + a_1 = 17
2a_1 + a_2 + a_3 + 12 = 17
2a_1 + a_2 + a_3 = 5
18. (a_2 + 4) + (a_3 + 4) + a_1 + a_2 = 18
a_1 + 2a_2 + a_3 + 8 = 18
a_1 + 2a_2 + a_3 = 10
19. (a_3 + 4) + a_1 + a_2 + a_3 = 19
a_1 + a_2 + 2a_3 + 4 = 19
a_1 + a_2 + 2a_3 = 15
From 1, a_4 = 1 - (a_1 + a_2 + a_3).
From 19, a_1 + a_2 + a_3 = 19 - a_19.
Substitute into 1:
19 - a_19 + a_4 = 1, so a_4 = a_19 - 18.
Since a_19 = a_3 + 4, a_3 = a_19 - 4.
From 1, a_1 + a_2 + a_3 = 1 - a_4 = 1 - (a_19 - 18) = 19 - a_19.
Now substitute a_3 = a_19 - 4 into a_1 + a_2 + 2a_3 = 15.
a_1 + a_2 + 2(a_19 - 4) = 15
a_1 + a_2 + 2a_19 - 8 = 15
a_1 + a_2 = 23 - 2a_19.
Substitute into a_1 + a_2 + a_3 = 19 - a_19.
23 - 2a_19 + a_19 - 4 = 19
19 - a_19 = 19
a_19 = 0.
Final Answer: The final answer is $\boxed{0}$
Question 1178476: According to the American Society of Heating, Refrigerating
and Air-Conditioning Engineers, Inc. (ASHRAE), a nonsmoking classroom
should have a ventilation rate of 15 ft3 per min for each person in the room.
(a) Write an equation that models the total ventilation V (in cubic feet per hour)
necessary for a classroom with x students.
(b) A common unit of ventilation is air change per hour (ach). One ach is equivalent
to exchanging all the air in a room every hour. If x students are in a classroom
having volume 15,000 ft3, determine how many air exchanges per hour (A) are
necessary to keep the room properly ventilated.
(c) Find the necessary number of ach (A) if the classroom has 40 students in it.
(d) In areas like bars and lounges that allow smoking, the ventilation rate should
be increased to 50 ft3 per min per person. Compared to classrooms, ventilation
should be increased by what factor in heavy smoking areas?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step:
**(a) Equation for Total Ventilation (V)**
* **Ventilation per person:** 15 ft³/min
* **Number of students:** x
* **Total ventilation per minute:** 15x ft³/min
* **Convert to cubic feet per hour:** 15x ft³/min * 60 min/hour = 900x ft³/hour
Therefore, the equation is:
* **V = 900x**
**(b) Air Exchanges per Hour (A)**
* **Total ventilation per hour:** V = 900x ft³/hour
* **Classroom volume:** 15,000 ft³
* **Air exchanges per hour (A):** A = (Total ventilation per hour) / (Classroom volume)
* **A = (900x) / 15,000**
* **A = 9x / 150 = 3x / 50**
Therefore, the number of air exchanges per hour is:
* **A = 3x / 50**
**(c) Necessary Air Exchanges with 40 Students**
* **Number of students (x):** 40
* **A = 3x / 50**
* **A = 3(40) / 50**
* **A = 120 / 50**
* **A = 12 / 5 = 2.4**
Therefore, with 40 students, 2.4 air exchanges per hour are necessary.
**(d) Ventilation Increase in Smoking Areas**
* **Ventilation in classrooms:** 15 ft³/min per person
* **Ventilation in smoking areas:** 50 ft³/min per person
* **Factor increase:** (Ventilation in smoking areas) / (Ventilation in classrooms)
* **Factor increase:** 50 / 15
* **Factor increase:** 10 / 3 ≈ 3.33
Therefore, ventilation should be increased by a factor of 10/3 or approximately 3.33 in heavy smoking areas.
Question 1184642: A landscaping supply company produces decorative stones. A ton of coarse stones requires 2 hours ofcrushing, 5 hours of sifting, and 8 hours of drying. A ton of fine stones requires 6 hours of crushing, 3hours of sifting, and 2 hours of drying. The coarse stones sell for$400 per ton. The fine stones sell for$500per ton. In a work week, the plant is capable of 36 hours of crushing, 30 hours of sifting, and 40 hours ofdrying. Based on the demand forecast, the quantity of coarse stones produced should be at least twice thequantity of fine stones produced.
First
1. Formulate an optimization model to decide how much of each kind of stones to produce to maximizetotal revenue.
2. Solve your model using the Excel solver.
3. Using a two-dimensional plot, solve your model graphically.
Then, by modifying your two-dimensional plot, answer the following questions:
4. How much would it be worth to get another hour of crushing time?
5. How much would it be worth to get another hour of sifting time?
6. Could you find the range of the prices for the fine stones such that in the optimal solution, thequantity of coarse stones produced is exactly twice the quantity of fine stones produced.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to formulate the optimization model, solve it using Excel Solver, and analyze it graphically:
**1. Optimization Model:**
* **Decision Variables:**
* x = Tons of coarse stones produced
* y = Tons of fine stones produced
* **Objective Function (Maximize Revenue):**
* Revenue = 400x + 500y
* **Constraints:**
* Crushing: 2x + 6y ≤ 36
* Sifting: 5x + 3y ≤ 30
* Drying: 8x + 2y ≤ 40
* Demand: x ≥ 2y
* Non-negativity: x ≥ 0, y ≥ 0
**2. Excel Solver Solution:**
1. Set up a spreadsheet with cells for x and y (the decision variables), the objective function (revenue), and each constraint.
2. Enter the coefficients for the objective function and constraints in the appropriate cells.
3. Use the SUMPRODUCT function to calculate the revenue and the left-hand side of each constraint.
4. Open the Solver add-in (Data tab > Solver).
5. Set the objective cell to the revenue cell, and select "Max."
6. Set the changing cells to the cells containing x and y.
7. Add the constraints by referencing the appropriate cells.
8. Select a solving method (Simplex LP is appropriate for this linear programming problem).
9. Click "Solve."
The Solver should give you the optimal values for x and y, as well as the maximum revenue. You'll likely find that x = 4 and y = 2, with a maximum revenue of $2600.
**3. Graphical Solution:**
1. **Plot the Constraints:** Treat each constraint as an equation and plot the lines on a graph with x and y axes. For inequalities, shade the feasible region.
2. **Identify the Feasible Region:** The feasible region is the area where all shaded regions overlap.
3. **Plot the Objective Function:** Pick an arbitrary revenue value and plot the line 400x + 500y = Revenue.
4. **Move the Objective Function Line:** Slide the objective function line parallel to itself in the direction of increasing revenue until it touches the last point of the feasible region. This point represents the optimal solution.
The intersection of the constraints x ≥ 2y, 2x + 6y ≤ 36, 5x + 3y ≤ 30, and 8x + 2y ≤ 40 will give you the feasible region. The optimal solution will be at the intersection of x = 2y, and 5x + 3y = 30, which is x = 4 and y = 2.
**4. Value of an Extra Hour of Crushing Time:**
1. Increase the crushing constraint to 2x + 6y ≤ 37 in your Excel model or adjust the graph.
2. Re-solve using Solver or graphically find the new optimal solution.
3. Calculate the difference in revenue between the new solution and the original solution. This is the "shadow price" or value of the extra crushing hour.
**5. Value of an Extra Hour of Sifting Time:**
1. Increase the sifting constraint to 5x + 3y ≤ 31.
2. Re-solve using Solver or graphically.
3. Calculate the difference in revenue.
**6. Range of Fine Stone Prices for x = 2y:**
1. Modify your Excel model to add a constraint that enforces x = 2y. You can do this by adding a cell with the formula x - 2y and setting the constraint as x - 2y = 0.
2. Re-solve and note the optimal revenue.
3. Change the price of fine stones (the coefficient of y in the objective function) and re-solve. Repeat this process, increasing and decreasing the fine stone price.
4. Observe the range of prices for which the optimal solution still maintains x = 2y. You'll find that there's a range of fine stone prices for which this relationship holds. If the fine stone price gets too high, the company will want to make more fine stones. If it gets too low, the company will want to make more coarse stones.
Question 1209593: Solve the system of equations
x + y + 2z = 1
-2x - 4y + 2z = 7
10x - 17x + 13z = 8
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Question 1209594: Solve the system of equations
5x + 3z = 1
-x + y - z = 0
2x - 3y + 7z = -4
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Since you did not tell us which method you have studied to use to solve systems,
I'll only give you the answers. If you want to know how to get them, then tell
us the method you were told to use and we'll help you.
The answers are:
Since you did not tell us which method you have studied to use to solve systems,
I'll only give you the answers. If you want to know how to get them, then tell
us the method you were told to use and we'll help you.
The answers are:
 Edwin
Edwin
Question 1185998: Solve for the unknown calories using the concept of linear equations
1.) 126x + 198y = 150
2.) 338x + 43y = 303
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this system of linear equations for x and y:
**Method 1: Substitution**
1. **Solve one equation for one variable:** It's easiest to solve the second equation for y:
43y = 303 - 338x
y = (303 - 338x) / 43
2. **Substitute:** Substitute this expression for y into the first equation:
126x + 198 * (303 - 338x) / 43 = 150
3. **Simplify and solve for x:**
126x + (60000 - 66924x)/43 = 150
5418x + 60000 - 66924x = 6450
-61506x = -53550
x = 53550 / 61506
x ≈ 0.872
4. **Substitute x back to find y:** Substitute the value of x into either original equation. Using the first equation is simplest.
126 * 0.872 + 198y = 150
110 + 198y = 150
198y = 40
y = 40 / 198
y ≈ 0.202
**Method 2: Elimination**
1. **Multiply equations to match coefficients:** We'll eliminate y. Multiply the first equation by 43 and the second equation by 198:
(126x + 198y = 150) * 43 => 5418x + 8514y = 6450
(338x + 43y = 303) * 198 => 66924x + 8514y = 60054
2. **Subtract the equations:** Subtract the first new equation from the second:
61506x = 53604
3. **Solve for x:**
x = 53604 / 61506
x ≈ 0.872
4. **Substitute x back to find y:** Substitute the value of x into either original equation.
126 * 0.872 + 198y = 150
y ≈ 0.202
**Solution:**
x ≈ 0.872
y ≈ 0.202
Question 1186000: Solve for the unknown calories using the concept of linear equations
1.) 126x + 198y = 150
2.) 338x + 43y = 303
With graphing method and subtitution, elimination, determinants
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve the system of equations using the methods you requested:
**1. Graphing Method:**
1. **Rewrite the equations in slope-intercept form (y = mx + b):**
* 126x + 198y = 150 => y = (-126/198)x + (150/198) => y ≈ -0.636x + 0.758
* 338x + 43y = 303 => y = (-338/43)x + (303/43) => y ≈ -7.86x + 7.047
2. **Plot the lines:** Graph both equations on the same coordinate plane. The point where the lines intersect is the solution.
3. **Approximate the solution:** From the graph, you'll see that the lines intersect somewhere around x ≈ 0.8 and y ≈ 0.3. Graphing isn't always perfectly precise, so these are just estimates.
**2. Substitution Method:**
1. **Solve one equation for one variable:** Let's solve the first equation for y:
y = (-126/198)x + (150/198)
2. **Substitute:** Substitute this expression for y into the second equation:
338x + 43((-126/198)x + (150/198)) = 303
3. **Simplify and solve for x:**
338x - (5418/198)x + (6450/198) = 303
(66864/198)x - (5418/198)x = (60054/198) - (6450/198)
(61446/198)x = (53604/198)
x = 53604 / 61446
x ≈ 0.872
4. **Substitute x back to find y:** Substitute the value of x into either of the original equations. Using the first equation is simpler.
126(0.872) + 198y = 150
110 + 198y = 150
198y = 40
y ≈ 0.202
**3. Elimination Method:**
1. **Multiply equations to match coefficients:** We want to eliminate either x or y. Let's eliminate y. Multiply the first equation by 43 and the second equation by 198:
* (126x + 198y = 150) * 43 => 5418x + 8514y = 6450
* (338x + 43y = 303) * 198 => 66864x + 8514y = 60054
2. **Subtract the equations:** Subtract the first new equation from the second:
61446x = 53604
3. **Solve for x:**
x ≈ 0.872
4. **Substitute x back to find y:** Substitute the value of x into either of the original equations.
126(0.872) + 198y = 150
y ≈ 0.202
**4. Determinant Method (Cramer's Rule):**
1. **Set up the coefficient matrix (D) and the matrices for x (Dx) and y (Dy):**
D = | 126 198 |
| 338 43 |
Dx = | 150 198 |
| 303 43 |
Dy = | 126 150 |
| 338 303 |
2. **Calculate the determinants:**
* det(D) = (126 * 43) - (198 * 338) = -61446
* det(Dx) = (150 * 43) - (198 * 303) = -53604
* det(Dy) = (126 * 303) - (150 * 338) = -12300
3. **Solve for x and y:**
x = det(Dx) / det(D) = -53604 / -61446 ≈ 0.872
y = det(Dy) / det(D) = -12300 / -61446 ≈ 0.200
**Solution:**
The solution using all methods converges to approximately:
* x ≈ 0.872
* y ≈ 0.202
Question 1186380: Ridership on a small regional airline has been declining, approximately at a linear rate. In 1981 the number of passengers was 245,000; in 1986 the number was 215,000. If n equals the number of passengers using the airline per year and t equals time measured in year (t=0 for 1981)
Determine the linear estimating function n=f(t)
Interpret the meaning of the slope
What is the number of riders expected to equal in the year 2000?
It is estimated that the airline will go out of business if ridership falls below 180,000. According to your function in part a, when will this happen?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**1. Determine the linear estimating function n = f(t):**
We are given two points on the line:
* (t₁, n₁) = (0, 245000) (1981)
* (t₂, n₂) = (5, 215000) (1986)
First, calculate the slope (m):
m = (n₂ - n₁) / (t₂ - t₁)
m = (215000 - 245000) / (5 - 0)
m = -30000 / 5
m = -6000
Now, use the point-slope form of a linear equation with one of the points (e.g., (0, 245000)):
n - n₁ = m(t - t₁)
n - 245000 = -6000(t - 0)
n = -6000t + 245000
So, the linear estimating function is: **n(t) = -6000t + 245000**
**2. Interpret the meaning of the slope:**
The slope, -6000, represents the average *decrease* in the number of passengers per year. In other words, the airline's ridership is declining by approximately 6,000 passengers each year.
**3. What is the number of riders expected in the year 2000?**
The year 2000 is 19 years after 1981 (2000 - 1981 = 19), so t = 19. Plug this into the equation:
n(19) = -6000 * 19 + 245000
n(19) = -114000 + 245000
n(19) = 131000
Therefore, the number of riders expected in the year 2000 is **131,000**.
**4. When will ridership fall below 180,000?**
We need to find the value of t when n(t) is less than 180,000:
180000 = -6000t + 245000
-65000 = -6000t
t = -65000 / -6000
t ≈ 10.83
Since t represents the number of years after 1981, we add this to 1981:
1981 + 10.83 ≈ 1991.83
Since we're dealing with whole numbers of years, ridership will likely fall below 180,000 in the year **1991** or **1992**.
Question 1209430: Solve 2x+y=8 and 3x-2y=5 using substitution method
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve 2x+y=8 and 3x-2y=5 using substitution method
~~~~~~~~~~~~~~~~~~~~~~
Your starting equations are
2x + y = 8 (1)
3x - 2y = 5. (2)
From equation (1), express y = 8 - 2x and substitute it into equation (2)
3x - 2(8-2x) = 5.
You have now one single equation for one unknown x.
Simplify and find x
3x - 16 + 4x = 5,
3x + 4x = 5 + 16
7x = 21
x = 21/7 = 3.
So, x is just found, x= 3.
Now substitute x = 3 in the first equation to find y
2*3 + y = 8,
y = 8 - 2*3 = 8 - 6 = 2.
ANSWER. The solution is this pair (x,y) = (3,2).
CHECK. Substitute these values x and y into equations to make sure
that left sides are equal to their right sides.
Solved.
Question 1209399: Find the ordered quintuplet (a,b,c,d,e) that satisfies the system of equations
a+2b+3c+4d+5e=41
2a+3b+4c+5d = 34
3a+4b+5c =15
4a+5b = 16
5a = 20
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Start at the bottom and work your way up.
5a = 20 means a = 4
4a+5b = 16 leads to 4*4+5b = 16 which yields b = 0
3a+4b+5c = 15 leads to 3*4+4*0+5c = 15 which yields c = 3/5
And so on.
The solution you should end up at is (a, b, c, d, e) = (4, 0, 3/5, 118/25, 408/125)
3/5 = 0.6
118/25 = 4.72
408/125 = 3.264
Each decimal value is exact and hasn't been rounded.
Question 1209394: Let x and y be complex numbers. If x + y = 2 and xy = 7 - x^2 - y^2, then what is x^2 + y^2?
Found 3 solutions by Edwin McCravy, math_tutor2020, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As the last tutor showed,
{x,y} = {3,-1} and x2 + y2 = 9 + 1 = 10
What the student should observe here is that
All REAL numbers ARE COMPLEX numbers!
3 and -1 are complex numbers because they are 3 + 0i and -1 + 0i respectively.
Nobody said the coefficient of " i " cannot be 0. And if it's 0, the number
is still complex. It's both REAL and COMPLEX.
Edwin
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 10
Work Shown
xy = 7 - x^2 - y^2
xy = 7 - (x^2 + y^2)
x^2 + y^2 = 7 - xy
2(x^2 + y^2) = 14 - 2xy
Let's call this equation (3)
x + y = 2
(x + y)^2 = 2^2
x^2 + 2xy + y^2 = 4
x^2 + y^2 = 4 - 2xy
Let's call this equation (4)
Subtract straight down for equations (3) and (4) to arrive at
x^2 + y^2 = 10
--------------------------------------------------------------------------
An alternative approach would be to rearrange x+y = 2 into y = 2-x
Then,
xy = 7-x^2-y^2
x(2-x) = 7-x^2-(2-x)^2
Solving that for x yields x = -1 and x = 3
I'll let the student handle the scratch work.
If x = -1 then y = 2-x = 2-(-1) = 3
If x = 3 then y = 2-x = 2-3 = -1
We get the same pair of values just in a different order.
Turns out the order doesn't matter.
Then,
x^2 + y^2 = (-1)^2 + (3)^2 = 10
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x and y be complex numbers. If x + y = 2 and xy = 7 - x^2 - y^2, then what is x^2 + y^2?
~~~~~~~~~~~~~~~~~~~~~~~~~~
.
x^2 + y^2 = add and subtract 2xy = (x^2 + 2xy + y^2) - 2xy = first parentheses is the square = (x+y)^2 - 2xy =
= substitute the given values = 2^2 - 2*(7-x^2-y^2).
Thus you have now
x^2 + y^2 = 4 - 14 + 2(x^2 + y^2),
x^2 + y^2 = -10 + 2(x^2 + y^2),
10 = x^2 + y^2.
At this point, the problem is solved completely.
ANSWER. x^2 + y^2 = 10.
Solved.
Question 1199840: ABC Dairy Company wishes to make a new cheese from two of its current cheeses: Cheese X and Cheese Y. The mixture is to weight at least than 4 pounds and is to contain 6 ounces of the sharpness Ingredients S. Each pound of X costs $4 and contains 3 ounces of S, whereas each pound of Y costs $1 and contains one ounce of S. find the minimum cost of the mixture if the amount of Cheese Y cannot exceed the amount of Cheese X by more than one pound.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Define Variables**
* Let 'x' be the amount of Cheese X in pounds.
* Let 'y' be the amount of Cheese Y in pounds.
**2. Formulate Constraints**
* **Weight Constraint:** x + y ≥ 4 (Total weight must be at least 4 pounds)
* **Sharpness Ingredient Constraint:** 3x + y ≥ 6 (Total amount of ingredient S must be at least 6 ounces)
* **Constraint on Cheese Y:** y - x ≤ 1
**3. Define Objective Function**
* **Cost Function (to be minimized):**
* Cost = 4x + 1y
**4. Graphical Representation**
* **Plot the constraints:**
* x + y ≥ 4
* 3x + y ≥ 6
* y - x ≤ 1
* **Find the feasible region:**
* The feasible region is the area on the graph that satisfies all the constraints simultaneously.
* **Identify the corner points of the feasible region.**
**5. Evaluate the Objective Function at Corner Points**
* Calculate the cost at each corner point of the feasible region.
**6. Determine the Minimum Cost**
* The corner point with the lowest cost value provides the minimum cost of the mixture.
**Note:**
* This problem can be solved graphically by plotting the constraints and finding the feasible region.
* Alternatively, you can use linear programming techniques (such as the simplex method) to find the optimal solution.
**To find the exact solution, you would need to:**
1. **Graph the constraints**
2. **Identify the feasible region**
3. **Determine the corner points**
4. **Calculate the cost at each corner point**
The corner point with the lowest cost will give you the minimum cost of the mixture and the optimal amounts of Cheese X and Cheese Y.
Question 1201735: Let X be the design matrix of a linear regression problem with m rows (samples) and d columns (variables/features). Let y∈R^m be the response vector corresponding the samples in X. Recall that for some vector space V⊆R^d the orthogonal complement of V is: V^⊥:={x∈R^d∣⟨x,v⟩=0∀v∈V}
1. Prove that: Ker(X)=Ker(X^⊤X)
2. Prove that for a square matrix A:Im(A^⊤)=Ker(A)^⊥
3. Let y=Xw be a non-homogeneous system of linear equations. Assume that X is square and not invertible. Show that the system has ∞ solutions ⇔y⊥Ker(X^⊤).
4. Consider the (normal) linear system X^⊤Xw=X^⊤y. Using what you have proved above prove that the normal equations can only have a unique solution (if X^⊤X is invertible) or infinitely many solutions (otherwise).
Please help me to solve question 3 and 4.
Answer by asinus(45)  (Show Source): (Show Source):
You can put this solution on YOUR website! Let's tackle each part of the problem step by step.
### 1. Prove that $ \text{Ker}(X) = \text{Ker}(X^TX) $
**Proof:**
- Let $ v \in \text{Ker}(X) $. Then, by definition, $ Xv = 0 $.
- Multiplying both sides by $ X^T $, we have:
$$
X^TXv = X^T0 = 0
$$
Thus, $ v \in \text{Ker}(X^TX) $.
- Now, let $ v \in \text{Ker}(X^TX) $. Then $ X^TXv = 0 $.
- This implies $ \langle Xv, Xv \rangle = 0 $ (since $ \langle a, a \rangle = 0 $ if and only if $ a = 0 $).
- Therefore, $ Xv = 0 $, which means $ v \in \text{Ker}(X) $.
Combining both parts, we conclude:
$$
\text{Ker}(X) = \text{Ker}(X^TX)
$$
### 2. Prove that for a square matrix $ A $: $ \text{Im}(A^T) = \text{Ker}(A)^\perp $
**Proof:**
- Let $ v \in \text{Im}(A^T) $. Then there exists some $ u $ such that $ v = A^Tu $.
- For any $ w \in \text{Ker}(A) $, we have $ Aw = 0 $.
- Thus, $ \langle v, w \rangle = \langle A^Tu, w \rangle = \langle u, Aw \rangle = \langle u, 0 \rangle = 0 $.
- This shows that $ v \in \text{Ker}(A)^\perp $.
- Now, let $ v \in \text{Ker}(A)^\perp $. We need to show $ v \in \text{Im}(A^T) $.
- By the definition of orthogonal complement, $ \langle v, w \rangle = 0 $ for all $ w \in \text{Ker}(A) $.
- The rank-nullity theorem states that $ \text{dim}(\text{Im}(A)) + \text{dim}(\text{Ker}(A)) = d $.
- Since $ A $ is square, $ \text{Im}(A^T) $ has dimension equal to $ \text{dim}(\text{Ker}(A)) $.
- Therefore, $ \text{Im}(A^T) = \text{Ker}(A)^\perp $.
### 3. Show that the system $ y = Xw $ has $ \infty $ solutions $ \Leftrightarrow y \perp \text{Ker}(X^T) $
**Proof:**
- If $ y \perp \text{Ker}(X^T) $, then for any $ v \in \text{Ker}(X^T) $, we have $ \langle y, v \rangle = 0 $.
- This means that $ y $ can be expressed as $ y = Xw + v $ for some $ w $ and $ v \in \text{Ker}(X^T) $.
- Since $ v $ can take infinitely many values in $ \text{Ker}(X^T) $, there are infinitely many $ w $ that satisfy $ y = Xw $.
- Conversely, if the system has infinitely many solutions, then there exists a non-zero $ v \in \text{Ker}(X^T) $ such that $ y = Xw + v $.
- This implies $ y \perp \text{Ker}(X^T) $.
Thus, we conclude:
$$
y \perp \text{Ker}(X^T) \Leftrightarrow \text{the system has } \infty \text{ solutions}
$$
### 4. Prove that the normal equations $ X^TXw = X^Ty $ can only have a unique solution (if $ X^TX $ is invertible) or infinitely many solutions (otherwise)
**Proof:**
- If $ X^TX $ is invertible, then the normal equations have a unique solution given by:
$$
w = (X^TX)^{-1}X^Ty
$$
- If $ X^TX $ is not invertible, then $ \text{Ker}(X^TX) \neq \{0\} $. From part 1, we know:
$$
\text{Ker}(X^TX) = \text{Ker}(X)
$$
- If $ y \perp \text{Ker}(X^T) $, then the system has infinitely many solutions, as shown in part 3.
Thus, we conclude:
- The normal equations have a unique solution if $ X^TX $ is invertible.
- They have infinitely many solutions if $ X^TX $ is not invertible.
This completes the proof for all parts.
Question 1205688: If T: R³→ R³ is If is a linear transformation defined by T(x,y,z)=(x+2y,x−y+z,−2y+z) Write the primary decomposition of R³
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the primary decomposition of R³ under the linear transformation T, we need to find the eigenvalues and eigenvectors of the matrix associated with T.
**Step 1: Find the Matrix Representation of T**
The matrix representation of T is:
```
A = [[1, 2, 0],
[1, -1, 1],
[0, -2, 1]]
```
**Step 2: Find the Eigenvalues of A**
To find the eigenvalues, we solve the characteristic equation det(A - λI) = 0:
```
det([[1-λ, 2, 0],
[1, -1-λ, 1],
[0, -2, 1-λ]]) = 0
```
Solving this equation, we find the eigenvalues: λ₁ = 1, λ₂ = -1, and λ₃ = 1.
**Step 3: Find the Eigenspaces**
For each eigenvalue, we find the corresponding eigenspace:
* **For λ₁ = 1:**
Solve the equation (A - I)v = 0:
```
[[0, 2, 0],
[1, -2, 1],
[0, -2, 0]]v = 0
```
The eigenspace E₁ is spanned by {(1, 0, 1), (0, 1, 1)}.
* **For λ₂ = -1:**
Solve the equation (A + I)v = 0:
```
[[2, 2, 0],
[1, 0, 1],
[0, -2, 2]]v = 0
```
The eigenspace E₂ is spanned by {(1, -1, 1)}.
**Step 4: Primary Decomposition**
Since the eigenvalues are distinct, the primary decomposition of R³ is the direct sum of the eigenspaces:
```
R³ = E₁ ⊕ E₂
```
where:
* E₁ = span{(1, 0, 1), (0, 1, 1)}
* E₂ = span{(1, -1, 1)}
This means that every vector in R³ can be uniquely expressed as a sum of a vector in E₁ and a vector in E₂.
Question 1209080: Seven years ago, Grogg's dad was 9 times as old as Grogg. Three years ago, Grogg's dad was 2 times as old as Grogg. How old is Grogg's dad currently?
Found 3 solutions by ikleyn, MathTherapy, math_tutor2020:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As two other tutors explained you, with the given input numbers, the answer is non-integer number,
which for this class of problems is traditionally considered as nonsense.
So, the problem is DEFECTIVE, and there is no sense to go further in more deep explanations.
************************************************************************
Simply throw this defective problem to the closest garbage bin.
It's a great pity for the wasted time.
************************************************************************
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Seven years ago, Grogg's dad was 9 times as old as Grogg. Three years ago, Grogg's dad was 2 times as old as Grogg.
How old is Grogg's dad currently?
That other person made things so COMPLEX. All he had to do was keep the ages CURRENT/"in-the-now", as was requested. What sense
does it make to solve for past ages when current ages are required? Inquiry minds want to know!!
Let Grogg's and his Dad's ages, be G and D, respectively
As such, 7 years ago, the Dad and Grogg were D - 7 and G - 7, respectively
Likewise, 3 years ago, the Dad and Grogg were D - 3 and G - 3, respectively
Then we get: D - 7 = 9(G - 7)____D - 7 = 9G - 63___D - 9G = - 56 ---- eq (i)
Also, D - 3 = 2(G - 3)___D - 3 = 2G - 6___D - 2G = - 3 ---- eq (ii)
Subtracting eq (i) from eq (ii), we get: 7G = 53
Grogg's current age, or G = 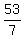 or or 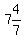 , which is a NON-INTEGER, and a seemingly NON-SENSICAL answer.
You could have also kept this to one variable: either G for Grogg's age, or D for his Dad's. , which is a NON-INTEGER, and a seemingly NON-SENSICAL answer.
You could have also kept this to one variable: either G for Grogg's age, or D for his Dad's.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
| 7 years ago | 3 years ago | | Grogg’s age | x | x+4 | | The dad’s age | 9x | 2(x+4) = 2x+8 |
7 years ago, Grogg's age was x years old.
His dad's age was 9x since its 9 times that of his son's age.
Fast forward 4 years so we arrive at the "3 years ago" timestamp.
At this point Grogg was x+4 years old and his dad was twice his age, so the dad was 2(x+4) = 2x+8 years old.
7 years ago the dad was 9x years old.
3 years ago the dad was 2x+8 years old.
This is a gap of 4 years, so subtracting these previous ages should get us 4.
(2x+8) - 9x = 4
Solving this equation leads to x = 4/7 = 0.571429 approximately
Since this isn't a whole number, there might be a typo somewhere in your question.
Question 1209192: A recipe calls for 3 2/3 cups flour AND sugar. The recipe only needs 1/4 c. of sugar. What is the total cups needed now.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As I read and re-read this post several times, every time I become laughing.
And I know that if I will re-read it 40 more times, I will laughing again and again.
Because the main idea and the major conception of the author is sticking out too much.
The main idea, the major conception and the greatest wish of the author of this post
is to confuse a reader. If to call the things by their proper names - his goal is to deceive the reader.
Dear author, the main idea and the major goal of mathematical problems
 is is  and and  . .
it is to give to a reader the best material to apply his/her knowledge,
to exercise and to learn something useful, as well as to develop his/her mind
from a problem posed by a clearest possible way.
From this post, it is obvious that
(1) the mathematical education of the problem's creator is from reading puzzles and comics, not from learning Math;
(2) knowing Math and knowing the proper Math style writing problems is at the zero level;
(3) this problem creator has no right idea, for what goal he creates his problems and disseminates them in the Internet.
Dear author, to be a successful Math problems composer, three things are needed:
- first, right selection and understanding of the goal;
- second, knowing the subject;
- and third, knowing in 10 times more than the subject.
And as a conclusion: the recipes similar to the described in this post, do not exist in the nature
and can not exist, because nobody in healphy mind will never read such gibberish and consider it as a receipt.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It's a shame that so many people don't know how to speak/write English....
"...3 2/3 cups of flour AND sugar..." means the TOTAL amount of flour AND sugar is 3 2/3 cups.
"What is the total cups needed now?"
What is the purpose of the "now" in that question? Nothing has happened; nothing in the statement of the problem says that any of the ingredients are changing or have changed.
The total cups needed, as stated in the first sentence, is 3 2/3 cups.
ANSWER: 3 2/3 cups
Question 1209072: Find the ordered pair (s,t) that satisfies the system
\frac{s}{2} + 5t = 3
3t - 6s = 9 + 15t + 11s
Found 2 solutions by mccravyedwin, Alan3354:
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
That notation is not compatible with the HTML this site is written in,
but from what I've learned, it means make a fraction with s as the
numerator and 2 as the denominator.
I won't solve it so another tutor can.
 Edwin
Edwin
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1209070: Find the ordered pair (x,y) that satisfies the system of equations
x + y = 15
x - y = 7 + 4x - 19y
Found 2 solutions by ikleyn, amarjeeth123:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let me tell you that this formulation in the post
"Find the ordered pair (x,y) that satisfies the system of equations"
is too wordy for Math and looks strange.
Word " ordered " is excessive.
Word " pair " is excessive.
Word " satisfies " is excessive.
Too many unnecessary words make writing unprofessional.
Much better is to say "Solve this system of equations".
Simple and convincing.
Answer by amarjeeth123(569)  (Show Source): (Show Source):
You can put this solution on YOUR website! The equations are as given below.
x + y = 15
x - y = 7 + 4x - 19y
These equations can be rewritten as given below.
x+y=15
-3x+18y=7
3x+3y=45
-3x+18y=7
21y=52
y=52/21
x=15-(52/21)=263/21.
Question 1209082: Real numbers a and b satisfy
a + ab^2 = 250b
a + b = 102
Enter all possible values of a, separated by commas.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Question 1209081: One ordered pair (a,b) satisfies the two equations ab^4 = 48 and a^2 b^3 = 24/b^5. What is the value of b in this ordered pair? (Note: you may have to use the Tab key to get your cursor into the middle answer box.)
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One ordered pair (a,b) satisfies the two equations ab^4 = 48 and a^2*b^3 = 24/b^5.
What is the value of b in this ordered pair?
(Note: you may have to use the Tab key to get your cursor into the middle answer box.)
~~~~~~~~~~~~~~~~~~~
Second equation is
a^2*b^3 =  ,
which is equivalent to
a^2*b^8 = 24. (1)
Compare it with the first equation
ab^4 = 48. (2)
Left side of (1) is the square of the left side of (2),
but right side of (1) is NOT the square of the right side of (2).
This contradiction shows and proves that the situation, described in the post,
NEVER may happen and, consequently, such ordered pair (a,b) DOES NOT exist. ,
which is equivalent to
a^2*b^8 = 24. (1)
Compare it with the first equation
ab^4 = 48. (2)
Left side of (1) is the square of the left side of (2),
but right side of (1) is NOT the square of the right side of (2).
This contradiction shows and proves that the situation, described in the post,
NEVER may happen and, consequently, such ordered pair (a,b) DOES NOT exist.
Solved, with complete explanations.
Question 1209084: For a certain value of k, the system
x + y + 3z = 10,
4x + 5y + 6z = 7,
kx - 3y + 2z = 3
has no solutions. What is this value of k?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1209071: Solve for (x,y) in the system of equations
2x + y = -7
x = 2y - 11 - 5x + 16y
Answer by ikleyn(52787)   (Show Source): (Show Source):
Question 1209073: For certain values of k and m, the system
a + 2b = -3
4a + 2b = k - 2a - mb + 6a + 2b + 5
has infinitely many solutions (a,b). What are k and m?
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For certain values of k and m, the system
a + 2b = -3
4a + 2b = k - 2a - mb + 6a + 2b + 5
has infinitely many solutions (a,b). What are k and m?
~~~~~~~~~~~~~~~~~~~~~~~~
Simplify second equation by combining common terms.
You will get an equivalent equation
0 = k - mb + 5. (*)
If m =/= 0, then this equation has a unique solution for "b"
b = 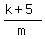 .
You then substitute this expression for "b" into the first equation and get a unique solution for "a".
So, if m =/= 0, you always has the unique solution to the system of equations.
The only case, when you have infinitely many solutions for "b", is the case m= 0.
Then k must be -5 , according to equation (*).
In this way, you get the
ANSWER. For m= 0 and k= -5, the given system has infinitely many solutions.
Conversely, in order for the given system has infinitely many solutions, "m" must be zero and "k" must be -5.
Thus the necessary and sufficient condition for the given system to have infinitely many solutions
is the condition m= 0, k= -5. .
You then substitute this expression for "b" into the first equation and get a unique solution for "a".
So, if m =/= 0, you always has the unique solution to the system of equations.
The only case, when you have infinitely many solutions for "b", is the case m= 0.
Then k must be -5 , according to equation (*).
In this way, you get the
ANSWER. For m= 0 and k= -5, the given system has infinitely many solutions.
Conversely, in order for the given system has infinitely many solutions, "m" must be zero and "k" must be -5.
Thus the necessary and sufficient condition for the given system to have infinitely many solutions
is the condition m= 0, k= -5.
Solved.
Question 1209074: At a store, you are interested in purchasing a candy bar and a piece of bubble gum. Together, they cost $1.20. The candy bar costs a dollar more than four times the bubble gum. How much does the piece of bubble gum cost, in cents?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
b = cost of bubble gum
4b+100 = cost of candy bar
Both costs are in cents.
candybar + gum = 120 cents
(4b+100)+b = 120
5b+100 = 120
5b = 120-100
5b = 20
b = 20/5
b = 4
The gum costs 4 cents.
4b+100 = 4*4+100 = 116 cents, aka $1.16, is the cost of the candy bar.
candybar + gum = $1.16 + $0.04 = $1.20 which confirms the answer is correct.
Answer: 4 cents
Question 1209008: Sophie's favorite number is a two-digit number. If she reverses the digits, the result is $45$ less than her favorite number. The sum of the digits in her favorite number is $6$. What is Sophie's favorite number?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Sophie's favorite number is a two-digit number. If she reverses the digits, the result is $45$ less
than her favorite number. The sum of the digits in her favorite number is $6$. What is Sophie's favorite number?
~~~~~~~~~~~~~~~~~~~~~~~~~
The given info that the difference of the number and the reversed number is 45
tells us that the difference of the digits is 45/9 = 5.
Hence, the digits are of different parity.
Then the sum of the digits can not be 6. Contradiction.
Beware of sending wrong tasks to this forum.
Avoid sending wrong tasks to this forum.
Big brother is watching everything you do here.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
For the original number we have
t = tens digit
u = units digit
That constructs 10t+u
For instance if the number is 23 then t = 2 and u = 3.
10t+u = 10*2+3 = 23.
The digits of Sophie's mystery number add to 6.
t+u = 6 which solves to u = 6-t
This will be useful in a substitution later.
10u+t is the result of reversing the digits. This is 45 less than her favorite number.
swapped = original - 45
10u + t = 10t+u - 45
10(u) + t = 10t+u - 45
10(6-t) + t = 10t+6-t - 45
60-10t+t = 10t+6-t-45
60-9t = 9t-39
-9t-9t = -39-60
-18t = -99
t = -99/(-18)
t = 5.5
We do not get a whole number result for the tens digit, so there must be a typo somewhere in your question.
Perhaps the digits add to something else other than 6?
Or maybe the "45" should be another value?
I would ask your teacher for clarification.
Question 1209007: Anna has a collection of $120$ marbles, each of which is either red or blue. If Anna has $135$ more red marbles than blue marbles, how many blue marbles does she have?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It recalls me a humoristic description of a mad-house in a classic novel of one classic author.
He describes a personage of this mad-house, who stated that inside of the Earth globe
there is another sphere of a greater diameter.
My lovely humor.
The blind begin to walk and the mute begin to see.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515
|





