Question 701371: How do I solve this linear equation 3x-y=4 and 7x-2y=13
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is a system of 2 linear equations with 2 variables. is a system of 2 linear equations with 2 variables.
You were probably taught about two ways to solve systems of 2 linear equations with 2 variables.
They are simple and easy to remember once you see them in action.
Both ways involve combining the two equations to make one equation that has only one variable ( or or  ). ).
You find that variable first, and then go back to the system to find the other variable.
For the system you ask about, both ways work equally well.
OPTION 1 (SUBSTITUTION):
Substitution is easy in some cases.
You have to know if that is the case, and you have to chose wisely the variable to be substituted.
Tip: look for a variable that does not have a visible coefficient in front.
Noticing that you see no coefficient in front of  in in  , ,
you find that it is easy to "solve for  " to find an expression equal to " to find an expression equal to 
Then, you can substitute that expression for  in the other equation to get an equation with only in the other equation to get an equation with only  for a variable. for a variable.
Step 1: "Solve for y", or "isolate y"
You work carefully from  to find that to find that
 . .
You "solved for y" by finding a "formula" to calculate  based on based on  . .
You "isolated y" on one side of the equal sign.
If you are not sure how to do that read the "Note 1:" below.
Step 2: Substitute that expression for  in the other equation. in the other equation.
Since you worked with  to find that to find that 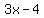 is the same as is the same as  , ,
now you go to the other equation,  , ,
and substitute 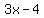 for for  . .
 --> -->  --> -->  --> -->  --> --> 
Step 3: Go back for 
You had found  as a "formula" to calculate as a "formula" to calculate  based on based on  . .
Now that you know that  , you use that formula. , you use that formula.
 --> -->  --> --> 
Step 4 (Optional): Verify by substituting the values you found for  and and  . .
I always do (because I know I make mistakes).
Does  with with  make make  equal to 4? equal to 4?
 YES! YES!
Does  with with  make make 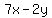 equal to 13? equal to 13?
 YES! YES!
Note 1:
How do you do "isolate y" and find that  ? ?
You could first add  to both sides and then subtract 4 from both sides: to both sides and then subtract 4 from both sides:
 --> -->  --> --> 
Or you could add 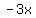 (also called subtract (also called subtract  ) from both sides and then multiply both sides times ) from both sides and then multiply both sides times  : :
 --> -->  --> --> 
Teacher may like the looks of  better, but better, but  and and  are the same thing. are the same thing.
OPTION 1 (ELIMINATION) (or COMBINATIONS):
Sometimes substitution makes you work with cumbersome fractions.
If I see that there are coefficients in front of every  and and  , ,
I do not try substitution.
I use elimination (also called combination of equations).
Step 1: Make your combination of equations so as to eliminate a variable.
That means that the combination equation must have only  , or only , or only  . .
You make a combination of the two equations by multiplying them times numbers and adding them.
You have to choose those numbers so as to eliminate a variable.
In this case, I would choose to eliminate 
by multiplying the first equation times 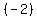 , ,
the multiplied first equation will have +2y,
while the other equation has -2y,
and adding then eliminates  . .
Your teacher may say think of that as multiplying the first equation times  and subtracting the result from the second equation. and subtracting the result from the second equation.
(I always add, because I make less mistakes that way).
It's really the same thing, but if your teacher does not like the way you do it,
agreeing with your teacher is a good strategy.
From  , multiplying both sides by , multiplying both sides by 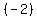 , you get , you get
 . .
(Multiplying times  would get would get  ). ).
I'll show you how I multiply in the "Note 2:" below
To combine the equations you may be expected to line them up one atop the other.
I do it because it makes seeing what I'm doing easier.
.. 

-----------------
..  --> --> 
The next step is to plug that value for  in one of the equations and solve for in one of the equations and solve for  . .
One easy option would be to use 
 --> -->  --> -->  --> -->  --> --> 
or, if you prefer,
 --> -->  --> -->  --> -->  --> -->  --> --> 
Note 2:
Here'e how I multiply an equation times a number.
I'm showing  times times 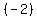 . .
I never write this all out; I just do it in my head,
and just write the end result.
At most, I would write:
 --(times(-2)--> --(times(-2)--> 
if I have to show what I am multiplying.
 --> -->  --> --> 
|
|
|